|
Uppgifter
hämtade från boken "Je mehr Löcher, desto weniger Käse"
("Ju fler hål, desto mindre ost") |
Uppg. 1: Talmysteriet
Lösning:
Enligt konjugatregeln är 42 - 32
= (4 + 3)(4 - 3) = 7
. 1 = 7
Om kvadraternas baser är positiva heltal, kan svaret därför fås fram som summan av kvadraternas baser
endast om differensen i den andra parentesen är 1.
Därför fungerar metoden för
112 - 102, 1002 - 992
osv. men inte för till exempel
112 - 92 och 1012 - 982.
|
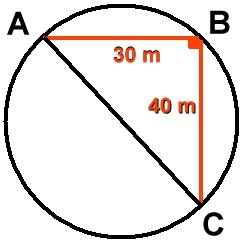
Uppg. 2: Simturen
Svar:
Diametern är 50 m
Lösning:
Vinkeln B är rät.
Enligt randvinkelsatsen är då AC en diameter i cirkeln.
(Jämför svarlatin.htm)
Med hjälp av Pytagoras sats beräknas sträckan AC (50 m).
|
 |
Uppg. 3: Primtalen
Svar: Det finns inga tresiffriga primtal, som uppfyller
villkoren.
Lösning:
Antag att den mellersta siffran är a.
Då är den första siffran a + 1 och den sista siffran a+2.
Talets siffersumma är a+ 1 + a + a + 2 = 3a + 3 = 3(a + 1).
Men enligt en känd regel är ett tal delbart med tre, om dess
siffersumma är delbar med tre.
När talet är delbart med tre, är det inget primtal!
Staffan R. har föreslagit följande lösning:
Eftersom den sista siffran
är två större än den mellersta kan den sista primtalssiffran
bara vara 3, 7 eller 9. Vi undersöker då talen 213, 657 och 879.
Alla tre är delbara med 3. De sökta primtalen finns inte. |
Uppg. 4: Talen 1 - 9
Svar:
Det finns två lösningar
1 + 5 + 9 = 2 + 6 + 7 = 3 + 4 + 8
1 + 6 + 8 = 2 + 4 + 9 = 3 + 5 + 7
Lösning:
Summan av talen 1 - 9 är 45.
Summan av de tre tal, som adderas, ska därför alltid bli 15.
Man inser lätt att talen 1, 2 och 3 måste tillhöra olika "tripplar",
om summan ska bli 15.
Talet 1 kan stå tillsammans med 5 och 9 eller tillsammans med 6
och 8.
Talet 2 kan stå tillsammans med 6 och 7 eller tillsammans med 4
och 9. |
Uppg. 5: Ekvationssystemet
 |
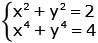(1) |
| (2) |
Lösning:
Kvadrera den första ekvationen
x4 + 2x2y2 + y4 = 4
Jämför denna ekvation med den andra ekvationen.
Då inser man att 2x2y2 = 0 och att x eller
y måste vara lika med noll.
Fall 1: x = 0 y = ±
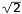(x = 0 insatt i den första ekvationen ger y-värdet)
Fall 2: x = ±
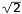y = 0 |
|