|
FLUGAN
|
Svar:
Flugan flög ungefär 121 m
Lösning:

När Lukas viftar undan flugan är
han i punkten L1 och Rasmus i punkten R1
Flugan hinner ikapp Rasmus i
punkten R2
vänder och möter Lukas i
punkten
L1.
Förhållandet mellan flugans och militärkolonnens hastighet
är proportionellt mot motsvarande sträckor:
1) Flugan
flyger
L1 => R2 när
Rasmus går R1 => R2 :
(50 + a)/a
2) Flugan flyger
L1 => R2 =>
L2 när Lukas går L1 => L2:
(50 + 2a)/50
Ekv.: (50 + a)/a =
(50 + 2a)/50
50/a + 1 = 1 + 2a/50
a2 = 1250
a = ±
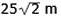
Flugan
flög 50 m + 2a m ≈ 121 m
|
>
|
|
|
skolpojkarna |
Svar:
a)
Adams skolväg: är 3,4 km
Bosses skolväg: är 2,2 km
b) Adam:
24 km/h
Bosse: 12 km/h
Christian:6 km/h
Lösning:
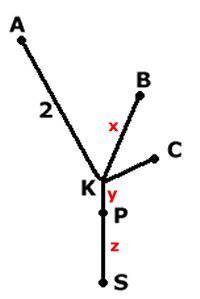
Jämför sträckorna för A och B
fram till P:
2 + y = 2(x + y) (1)
Jämför sträckorna för A och C fram till P:
2 + y
= 4(1,6 - z) (2)
Sammanlagt för alla tre fram till punkten P:
2
+ x + 2y + 1,6 - z = 4,2 (3)
Efter förenkling:
2x + y = 2 (1)
y + 4z = 4,4
(2)
x + 2y - z = 0,6 (3)
Eliminera z
4x +
9y = 6,8 (4)
(1) och (4) ger efter förenkling:
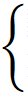 |
x
= 0,8
y = 0,4
Enl. (3) är z = 1 |
a)
Adams skolväg: (2 + 0,4 + 1) km = 3,4 km
Bosses skolväg: (0,8 + 0,4 + 1) km = 2,2 km
b)
Antag att Christians är v
km/h och
Adams hastighet 4v
km/h 7,5 min = 1/8 h
Använd formeln t
= s/v för sträckan PS.
Ekv.: 1/v = 1/4v +1/8
Christian: v = 6 (km/h)
Adam:
4v = 24 (km/h)
Bosse: 2v = 12 (km/h)
|
|
|
|
|
LOTHRINgSKA KORSET |
Svar:
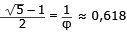
Lösning:
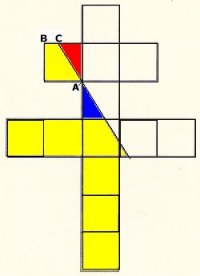
Hela
korset består av 13 kvadrater.
Om man
flyttar den blå triangeln till den röda triangelns
plats, har man sammanlagt mer än 6,5 färgade
kvadrater.
|
 |
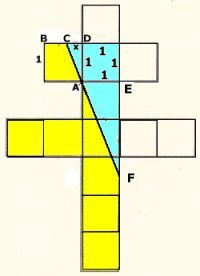 |
Linjen från C genom A är därför inte korrekt. Figuren till
höger verkar rimligare.
Triangeln AEF är likformig med
triangeln ACD. CD = x
EF/1 = 1/x
EF = 1/x
Ekvation för den gula arean: De färgade kvadraternas area -
den gröna arean.
9 - (x + 1)(1 + 1/x)/2 = 6,5
Efter förenkling
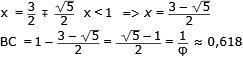
φ är tecknet för fi ≈ 1,618 (Gyllene snittet)
|
|
yin och yang |
Svar:
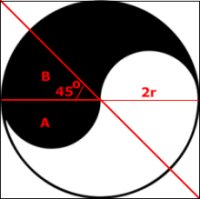
Ja, dra den röda diagonalen
Lösning:
Henry Dudeney hade ett ganska
krångligt bevis till det här problemet.
Ett enklare bevis
kan se ut så här:
Arean av den stora cirkeln: 4 r2 r2
Då är Yin 4 r2/2
= 2 r2/2
= 2 r2 r2
Till vänster om den röda delningslinjen ska arean av Yin
vara  r2 r2
Halvcirkeln A:
 r2/2 r2/2
Cirkelsektorn B ska därför vara
 r2
- r2
-
 r2/2
= r2/2
=
 r2/2 r2/2
Det är den om medelpunktsvinkeln för cirkelsektorn B är 45o.
4 r2
. 45/360 = r2
. 45/360 =
 r2/2 r2/2
Med samma typ av bevis visar man att Yang delas mitt itu av
den röda linjen.
|
 |
|
|
|
|
|
ETT FÅRAKTIGT PROBLEM |
|
Svar:
Två dollar
Lösning:
Antag att fadern efterlämnade x får och att bröderna
sedan köpte y får och att lammet kostade z dollar. z <
10 dollar
Ekv.: x2
= 10y + z
y är ett udda tal, eftersom y + 1 (lammet)
är ett jämnt tal.
Det innebär att den näst sista
siffran i x2 är udda.
Undersök x2
för olika värden av x:
|
x |
x2 |
x |
x2 |
|
|
4 |
16 |
11 |
121 |
Av tabellen framgår att |
| 5 |
25 |
12 |
144 |
näst sista siffran i x2 är |
|
6 |
36 |
13 |
169 |
udda endast om den |
| 7 |
49 |
14 |
196 |
sista siffran (= z) är 6. |
| 8 |
64 |
15 |
225 |
Den ena brodern måste |
| 9 |
81 |
16 |
256 |
lämna över 2 dollar. |
| 10 |
100 |
|
|
(10 - 2 = 6 + 2) |
|
|