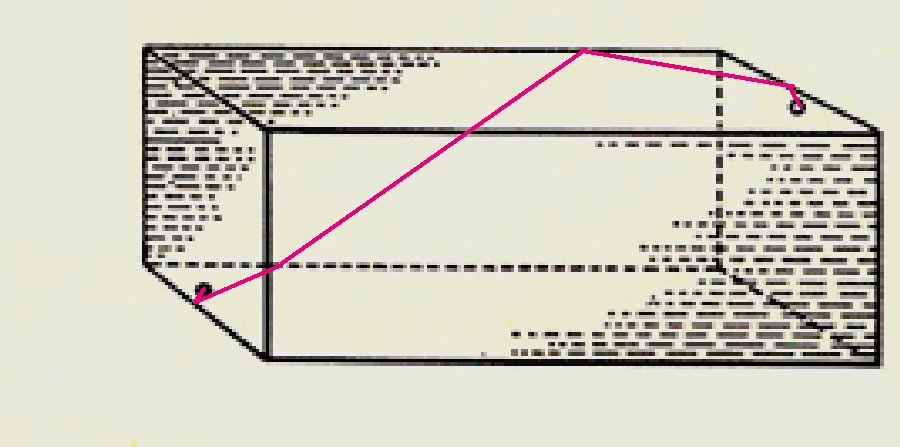
Spindeln och flugan (eller... "när spindeln gick i taket")

Svar: Avståndet är 40 fot.

Lösning:
För att kunna hitta den kortaste vägen måste man "vika ut" golv, väggar och tak, så att de alla ligger i samma plan. Det kan göras på flera olika sätt, så det gäller att kolla vilket alternativ som ger det kortaste avståndet. I "3D-problem nr 1" (Klurigt 2) ges exempel på hur ett rätblock kan vikas ut.

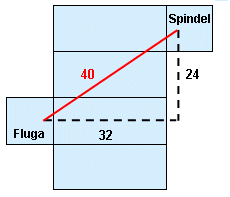
I fig. uppe till höger visas hur utvikningen skall göras. Pytagoras sats ger sedan avståndet (x): x²=24²+32² osv.

Tillbaka

Tudelning

Bevis:
Det svarta och vita området är kongruenta (vridning 180^o runt den stora cirkelns medelpunkt). Man kan också inse detta genom att flytta den svarta "spejade" halvcirkeln till den vita "sprejade" halvcirkeln.

Antag att radien i den stora cirkeln är 2 (l.e.) och att radien i de små halvcirklarna är 1 (l.e.)
Den stora cirkelns area är då 2^.2^. p = 4p (a.e.) 
Påst.: Arean av den del av det svarta området som ligger till vänster om den röda diagonalen är 1/4 av den stora cirkelns area, dvs. p (a.e.). 
Bevis:
Den lilla halvcirkelns area är 1^.1^. p/2  = p/2 (a.e.)
Cirkelsektorn med 45^o medelpunktsvinkel har arean 2^.2^. p/8  = p/2 (a.e.)
Sammanlagd area: p/2 + p/2 =  p (a.e.) V.S.B.