Klurigt nr 14 (lösningar)

Varudeklaration 1 

Svar: 0 Lösning: 15 . 14 .  12 . 9 . 5. 0. .... = 0

Problem för färgblinda? 

Svar: 3/4 av rektangeln är färgad.

Farfar 

Svar: 60 år Lösning: När Johanna föddes, måste farfaderns ålder ha varit jämnt delbar med 2, 3, 4, 5 och 6. Mgn.: 60.

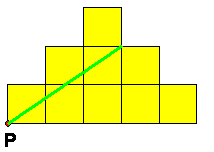
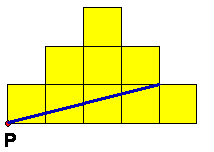
Delikat delning

Svar: Det finns två  lösningar (Se fig.)

Varudeklaration 2 

Svar: 50 Parentesuttrycken kan enklare skrivas Efter förkortning får man

Tre hjärter 

Svar: De andra två korten är hjärter fyra och hjärter sex, eftersom Anna måste ha haft hjärter tre! Bevis:  Om Annas kort är hjärter två, finns det flera  kombinationer som ger summan 13. Anna kan då inte ange valören på de andra korten. Annas kort kan inte ha en högre valör än 3, eftersom summan i så fall skulle skulle bli större än 13. Ex.: 4+5+6=15 Om Annas kort är hjärter tre, finns det bara en möjlig kombination: 3+4+6=13. Därför kan Anna tala om att de övriga korten är hjärter fyra och hjärter sex.

Rulltrappan 

Svar: 40 s Lösning:  Antag att rulltrappan är x m. 1)  När Lena går uppför den stillastående rulltrappan är hennes hastighet x/104 m/s  2) Rulltrappans hastighet är x/65 m/s 3) När Lena går uppför den fungerande rulltrappan blir hastigheten  (x/65 + x/104) m/s. Tiden blir då x/(x/65 + x/104) s = 40 s.

Problem i kvadrat 2 

Svar: 242 242 + 242 = 484 = 222 Anm. 1: Om villkoret inte är att det tresiffriga talet skall vara en palindrom, finns det betydligt fler lösningar! Se tabellen till höger.  Anm. 2: I tabellen till höger får man summorna 121=112  484=222  1089=332 och 625=252.

110 11 440 44 143 341 461 164 164 461 495 594 198 891 560 65 242 242 594 495 263 362 693 396 297 792 792 297 341 143 891 198 362 263 990 99 396 693

Professor Kalkyls bröllopsdag

Svar: a) 35 år Vi börjar med att undersöka summan av kuberna på de första udda primtalen - det jämna primtalet 2 bryr vi oss således inte om. 33 + 53 = 27 + 125 = 152 33 + 53 + 73 = 27 + 125 + 343 = 495 33 + 53 + 73 +113 = 27 + 125 + 343 + 1331 = 1826 33 + 53 + 73 +113 +133 = 27 + 125 + 343 + 1331 + 2197= 4023 Summan av kuberna skall motsvara antalet veckor som prof. Kalkyl varit gift. En uppskattning av antalet år får vi genom att dividera med 52. 152/52 » 2,92     495/52 » 9,52      1826/52 » 35,12       4023/52 » 77,37  Endast det tredje alternativet är värt att undersöka närmare. Antag att prof. Kalkyl skall fira sin 35-åriga bröllopsdag. Det betyder att han gifte sig 1968. Om han gifte sig efter den 28 februari har han som gift upplevt 8 skottdagar. Han har då varit gift i (35*365 + 8) dagar = 12783 dagar. Om han firar sin bröllopsdag en dag för tidigt har han varit gift i (12783-1)/7 veckor =1826 veckor! Anm.: Om prof. Kalkyl hade varit född 100 år tidigare, hade han på sin 35-åriga bröllopsdag varit gift exakt 1826 veckor, eftersom år 1900 till skillnad från år 2000 inte är skottår! Svar: b) Efter 35 år firar man korallbröllop och därför tyckte väl prof. Kalkyl att det var lämpligt att åka till Stora Barriärrevet, som är jordens längsta korallrev.

Ett fantastiskt korttrick

Lösning

Referenser:
Michael Cleber (Mathematical Intelligencer 2002): The best card trick.
Ian Stewart (New Scientistic 2003): It´s a kind of magic.

 

För denna sida ansvarar: Alf Gunnarsson

|Tillbaka |