Ett möbiusband är en lång rektangulär yta, som vridits ett halvt varv innan ändarna sätts ihop.
Se mobius.htm
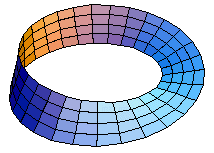
Klurigt nr 3
| Möbiusband Ett möbiusband är en lång rektangulär yta, som vridits ett halvt varv innan ändarna sätts ihop. Se mobius.htm |
|
| Använd
miniräknare för att beräkna 5*15469. Vänd miniräknaren upp och ner. Med lite fantasi kan du då läsa namnet på ett oljebolag. Uppgifter: Konstruera räkneuppgifter som (med miniräknaren upp och ner) ger ett ord som svar, t.ex. a) hes b) hiss c) seg d) sill e) silo |
| a) Den 2 februari 2000
var det första gången på mycket länge som man kunde skriva dagens datum
(2000-02-02) genom att enbart använda jämna tal. När inträffade det
senast? b) Det kommer att dröja många år innan man kan skriva ett datum utan nollor. Ange detta datum! |
Sannolikhet
|
Johanna Svensson har två barn. Det äldre av dem heter Erik. Hur stor
är sannolikheten att båda är pojkar? Sofia Karlsson har också två barn. Ett av dem heter Erik. Hur stor är sannolikheten att båda är pojkar? |
 |
Fyra stengetter
gick genom ett mycket trångt alppass med lodräta väggar. Plötsligt mötte de
fyra andra stengetter. Stengetter är inte bara duktiga att klättra och
hoppa. De är också envisa! När de båda grupperna av stengetter var på en stengets avstånd från varandra stannade de. |
|||||||||||||||
| Det var
otänkbart att någon skulle backa. Däremot kunde en stenget tänka sig att gå
framåt eller att hoppa över en stenget om det fanns en ledig plats på andra
sidan den "överhoppade" stengeten. Visa hur stengetterna skall göra för att
passera varandra. Ett litet tips: Låt tändstickor föreställa stengetter (se fig.) |
||||||||||||||||
| Sista bussen för
kvällen var fullsatt. Vid hållplats nr 1 steg en person samt 1/8 av resterande antal passagerare av. Vid hållplats nr 2 steg två personer plus 1/8 av resterande antal passagerare av osv. |
|
|
| De sista
passagerarna steg av vid den sista hållplatsen. Samma antal
passagerare steg av vid varje hållplats. a) Hur många passagerare var det från början i bussen? b) Hur många hållplatser var det? Ledning |
||
| En
gammal dam var på väg till kyrkogården för att sätta blommor på tre
gravar. När hon kom till den första graven, upptäckte hon en liten damm.
Hon doppade blommorna i dammen och när hon tog upp dem, hade hon dubbelt
så många blommor - det var en förtrollad damm! Hon satte några blommor på den första graven och gick vidare till nästa grav. Där fanns det också märkligt nog en damm! Hon doppade blommorna i dammen och när hon tog upp dem, hade antalet blommor fördubblats. Hon satte några blommor på graven och fortsatte sedan till den tredje graven. Även där fanns det en förtrollad damm. Än en gång fördubblades antalet blommor, när hon doppade dem i dammen. Den gamla damen satte nu alla sina återstående blommor på den tredje graven. Hur många blommor hade hon från början? Hur många blommor satte hon på varje grav? (Hon hade faktiskt utan att tänka på det satt lika många blommor på varje grav.) Ledning |
| För denna sida ansvarar: Alf Gunnarsson |