UTMANING - GEOMETRI

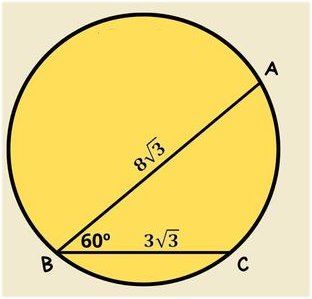
CIRKELNS DIAMETER

Beräkna cirkelns diameter!
Alla mått är angivna i cm.

  
 

VINKELN X

O är medelpunkt i cirkeln och PR är tangent till cirkeln.
Hur många grader är vinkeln x?

  
 

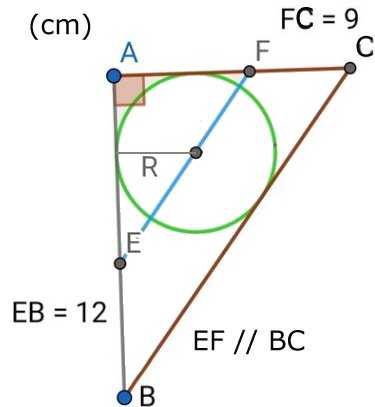
ETT VINKLAT PROBLEM

Sträckorna AC och AF är lika långa. Beräkna vinkeln v.

  

STRÄCKAN BC

I cirkelkvadranten dras de vinkelräta sträckorna AD och DC.
Hur lång är sträckan BC?

  
 

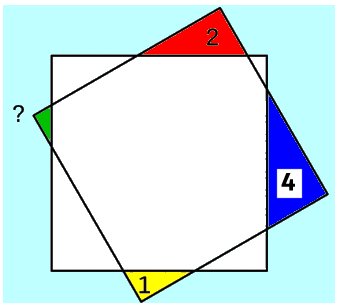
BEVIS

Figuren till höger är en kvadrat.
Bevisa att a2 + c2 = b2 + d2.

  
 

STRÄCKAN EF

I kvadraten ABCD finns två halvcirklar samt en linje EF, som går genom halvcirklarnas tangeringspunkt.
Beräkna längden av sträckan EF.

  

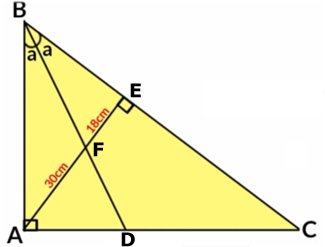
TRIANGELNS AREA

Bisektrisen BD delar sträckan AE i två delar, 30 cm och 18 cm.
Beräkna arean av triangeln ABC.

  
 

MAXIMAL AREA

I kvadraten ABCD är sidan a.
Från hörnet D dras en rät linje till punkten E på sidan AB och från E en rät linje till punkten F på BC så att vinkeln DEF är rät.
Beräkna förhållandet AE:EB när triangeln BEF har maximal area.

STRÄCKAN X

ABCD är en kvadrat med arean 24 cm2.
Beräkna den blå arean.

Lösning

 

 

TRIANGELNS AREA

Beräkna arean av triangeln FGH.

Lösning

 

 

 

 

  

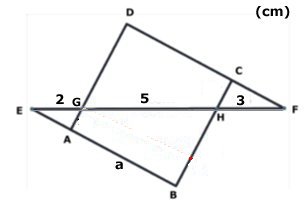
 KVADRATENS AREA

ABCD är en kvadrat.
EG = 2 cm, GH = 5 cm, HF = 3 cm.
Beräkna arean av ABCD.
 

Lösning

 

 

 

 

 

  

STRÄCKAN BE 

Beräkna sträckan BE!
 

Lösning

 

 

 

 

 

  

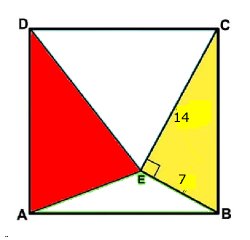
TRIANGELAREAN
ABCD är en kvadrat.
Beräkna arean av den röda triangeln.

Lösning

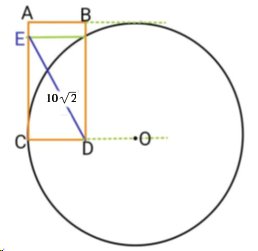
AREAN AV ABCD
 Beräkna arean av rektangeln ABCD.
Längden av sträckan DE framgår av figuren.

Lösning

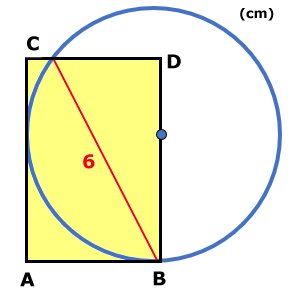
REKTANGELNS AREA I
 Beräkna arean av rektangeln ABCD.

Lösning

HALVCIRKLARNA
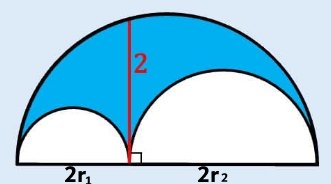
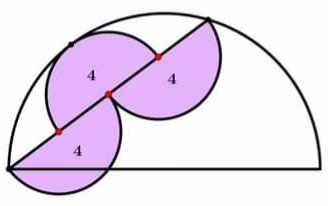
De tre små halvcirklarna har arean 4 cm2
Hur stor är arean av den stora halvcirkeln?

Lösning

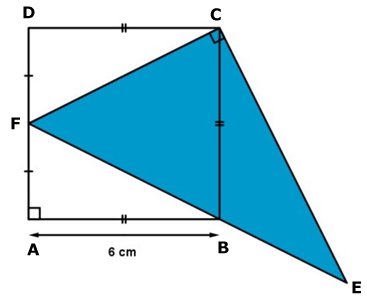
DEN BLÅ TRIANGELN
ABCD är en kvadrat med sidan 6 cm.
F är mittpunkt på sidan AD.
Beräkna arean av den blå triangeln.

Lösning

 		  

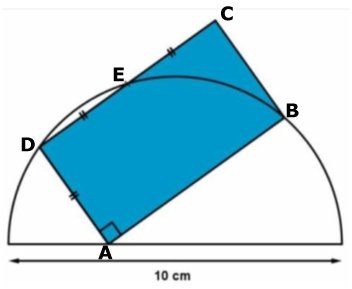
REKTANGELNS AREA II
I rektangeln ABCD är
AD = DE = EC.
Halvcirkelns diameter är
10 cm.
Beräkna rektangelns area.

Lösning

 

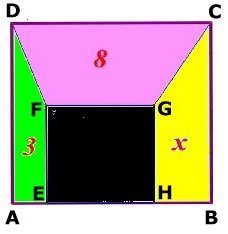
DEN GULA AREAN
ABCD och EFGH är kvadrater.
Den violetta arean är 8 cm2 och gröna arean är 3 cm2.
Hur stor är den gula arean?

Lösning
 

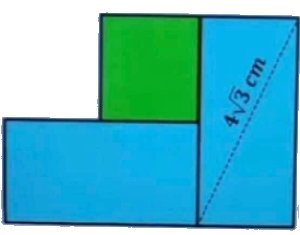
SAMMANLAGDA AREAN
De två blå rektanglarna är kongruenta och den gröna fyrhörningen är en kvadrat.
Hur stor är den sammanlagda arean av de tre fyrhörningarna?

Lösning

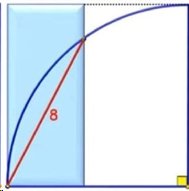
DEN BLÅ REKTANGELN
   
Beräkna arean av den blå rektangeln.
Den röda kordan i kvartscirkeln är 8 cm.

Lösning
 

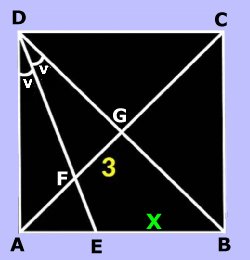
STRÄCKAN X
I kvadraten ABCD är stråckan FG 3 cm.
Beräkna sträckan X.
Lösning
 

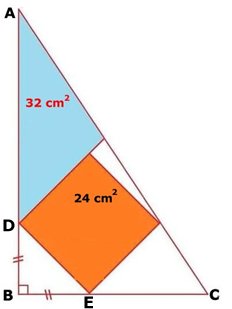
HUR STOR ÄR TRIANGELNS AREA?
I den stora triangeln finns bl.a. en blå triangel (32 cm2) och en brun kvadrat (24 cm2).

Sträckan BD = sträckan BE.

Hur stor är triangeln ABC:s area?

 Lösning
 
     

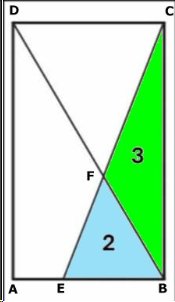
REKTANGELNS AREA III
Triangeln BEF har arean 2 cm2 och triangeln BCF 3 cm2.
Beräkna rektangelns area.

Lösning

RÄTVINKLIG TRIANGEL
Beräkna triangelns sidor.

Lösning

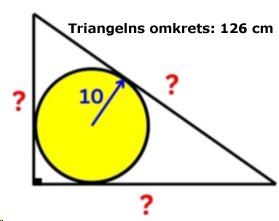
RADIEN
Beräkna cirkelns radie!

Lösning