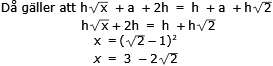UTMANING - GEOMETRI (LÖSNINGAR)
|
CIRKELNS DIAMETER |
|
|
Svar: Cirkelns
diameter är 14 cm. |
 |
|
VINKELN X |
|
|
Svar: Vinkeln X är
30o |
 |
|
ETT VINKLAT PROBLEM |
|
|
Svar: Vinkeln v är
30o |
 |
|
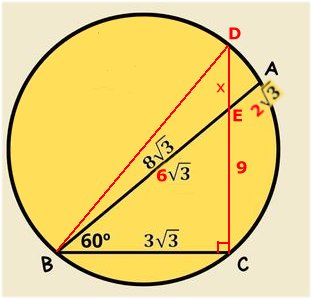
STRÄCKAN BC |
|
|
Svar: Sträckan BC är 15
cm |
 |
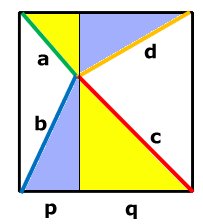
BEVIS
|
Bevis: |
p q
 |
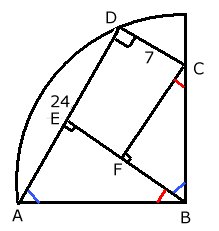
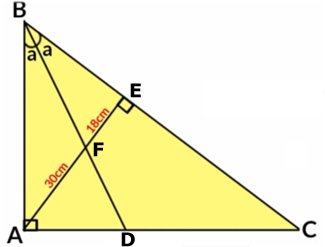
STRÄCKAN EF
|
Svar:
Sträckan EF är 18 cm. |
 |
TRIANGELNS AREA
|
Svar:
2400 cm2 |
 |
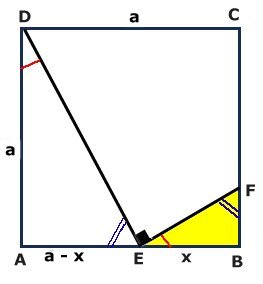
MAXIMAL AREA
| Svar:
AE:EB = 1:2 Lösning: Antag att sträckan EB är x cm. Då är sträckan AE (a - x) cm. Eftersom vinkeln DEF är rät, är det lätt att visa att triangeln BEF är likformig med triangeln ADE. Likformighet ger: x/a = BF/(a - x) BF = (ax - x2)/a  Tillbaka |
 |
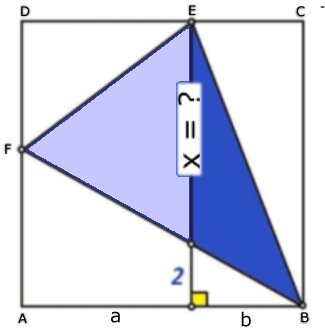
STRÄCKAN X
| Svar:
Den blå sträckan är 6 cm2 Lösning: Den ljusblå triangeln Basen är x och höjden a Area: x . a /2 Den mörkblå triangeln Area: x . b /2 Hela den blå triangeln Area: x(a + b)/2 (= 24 cm2 enl. texten i uppgiften) men a + b = x + 2 Alltså kan vi skriva x(x + 2)/2 = 24 x2 + 2x = 48 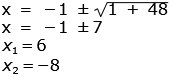 Tillbaka |
 |
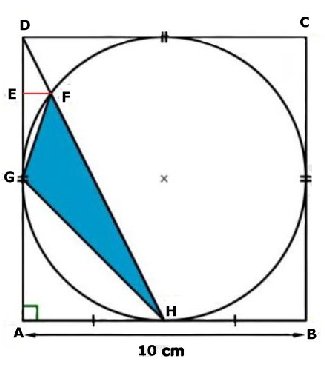
TRIANGELNS AREA
| Svar:
Triangeln FGH:s area är 10 cm2 Lösning: Pythagoras sats på triangeln ADH: (AD)2 + (AH)2 = (DH)2 102 + 52 = (DH)2 DH = Kordasatsen ger: DF . DH = (DG)2 DF . DF = Triangeln DEF är likformig med triangeln DAH. (EF)/(AH) = (DF)/(DH) EF = EF = 1 Arean av triangeln FGH = ADH -AGH - DFG = 25 - 12,5 - 2,5 = 10 (cm2) Tillbaka |
 |
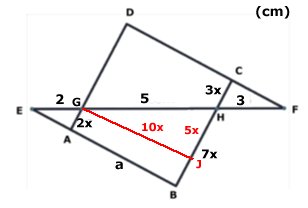
KVADRATENS AREA
| Svar:
Kvadratens area är 20 cm2 Lösning: EG = 2 cm, GH = 5 cm, HF = 3 cm. Trianglarna AEG, BEH och CFH är likformiga. Antag att AG är 2x. Då är CH = 3x och BH = 7x. Kvadratens sida a = BC = 10x Kvadratens area är (10x)2 = 100 x2 Pythagoras sats på triangeln GHJ ger: (5x)2 + (10x)2 = 52 125 x2 = 25 Då är 100x2 = 4 . 25/5 = 20 (cm2) Tillbaka |
 |
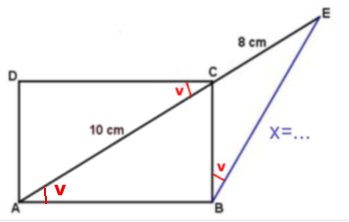
STRÄCKAN BE
| Svar:
Sträckan BE är 12 cm Lösning: Vinkeln BAC = vinkeln ACD (alternatvinklar) Triangeln BCE är likformig med triangeln ABE. (Likvinkliga trianglar: Vinkeln E är gemensam och båda trianglarna har en vinkel som är v grader). Likformighet ger: x/18 = 8/x x2 = 144 x = ± 12 Sträckan BE är 12 cm Tillbaka |
 |
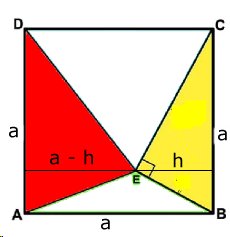
TRIANGELAREAN
 |
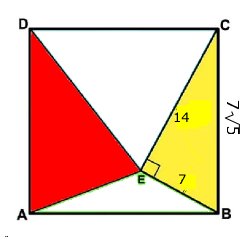 |
| Svar: Den
röda triangelns area är 73,5 cm2 Lösning: Påst.: Den röda och gula triangeln har en sammanlagd area = halva kvadraten. Bevis: Kvadratens area: a2 Trianglarnas area: a(a - h)/2 + ah/2 = a2/2 V.S.B. Tillbaka |
 |
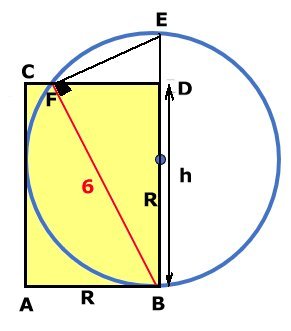
REKTANGELNS AREA I
| Svar:
Rektangelns area är 18 cm2 Lösning: Låt AC = h och cirkelns radie = R Då är rektangelns area = AB . AC = Rh Triangeln BDF är likformig med triangeln BFE. Likformighet ger: BD/BF = BF/BE h/6 = 6/2R Rh = 18 = rektangelns area Tillbaka |
 |
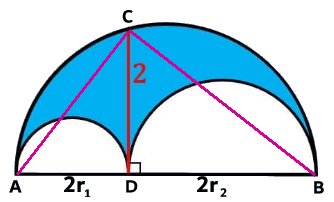
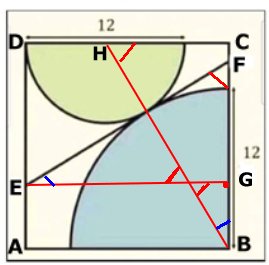
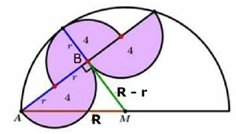
HALVCIRKLARNA
| Svar:
Lösning: Antag att radien i den stora halvcirkeln är R och i de små halvcirklarna r. Liten halvcirkel: r2 Triangeln ABM är rätvinklig. AB = 2r BM = R - r AM = R Pythagoras sats: (2r)2 + (R - r)2 = R2 4r2 + R2 - 2Rr + r2 = R2 5r2 - 2Rr = 0 r(5r - 2R) = 0 r1 = 0 r2 = 2R/5 => R = 5r/2 Stora halvcirkelns area: R2 Men r2 Då är 25r2 Tillbaka |
 |
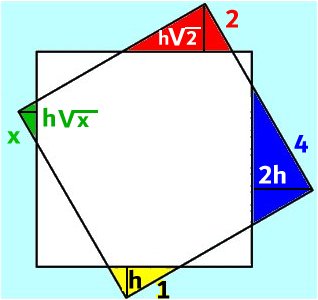
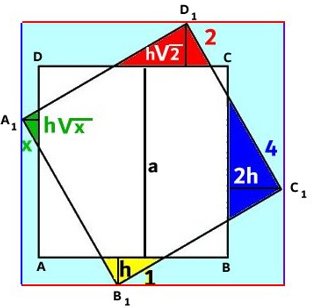
DEN BLÅ TRIANGELN
Svar: Triangelns area är 30 cm2 Lösning: Triangeln CDF är kongruent med triangeln ABF. Arctan vinkeln CFD = 6/3 Vinkeln CFD = vinkeln AFB Då är vinkeln BFC = 180o - 2 . arctan 6/3 ≈ 53,13o Då är den rätvinkliga triangeln CEF en egyptisk triangel, där sidorna förhåller sig som 3:4:5 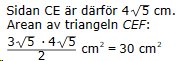 Tillbaka |
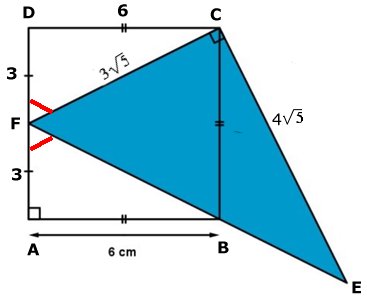 |
REKTANGELNS AREA II
| Svar:
Lösning: Rektangeln ABCD: Låt AB = a. Då är BC = AD = 2a. Vinklarna, som är markerade med två blå streck är lika stora (verikalvinklar). Pythagoras sats på trianglarna ABC och AEC ger: (AC)2 = 5a2 och (AC)2 = 50 Då är 5a2 = 50 a2 = 10 Rektangelns area: a . 2a = 2a2 a2 = 10 => 2a2 = 20 (cm2) Bevis saknas för att vinkeln AEC är 90o Tillbaka |
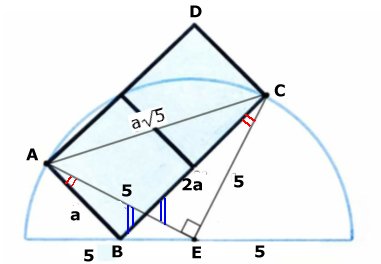 |
DEN GULA AREAN
| Svar: 5 cm2 Lösning: Antag att sidan i kvadraten ABCD är a cm och att sidan i kvadraten EFGH är b cm. Parallelltrapetset CDFG: Arean = (a + b)(a - b)/2 (a + b)(a- b)/2 = 8 a2 - b2 = 16 (!) Arean av kvadraten ABCD ger ekvationen: a2 = b2 + 8 + 3 + x a2 - b2 = 8 + 3 + x men a2 - b2 = 16 enligt (1) 16 = 8 + 3 + x x = 5 Tillbaka |
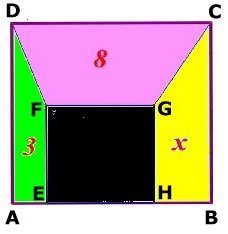 |
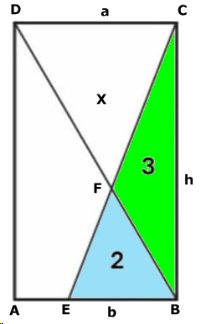
SAMMANLAGDA AREAN
| Svar:
48 cm2 Lösning: Rektanglarna har sidorna a och b cm. Kvadraten har sidan (b - a) cm. Pytagoras sats på triangeln ABC ger: a2 + b2 = ( a2 + b2 = 48 (1) Sammanlagd area: 2ab + (b - a)2 = = 2ab + b2 - 2ab + a2 a2 + b2 = = 48 enligt ekv. (1) Tillbaka |
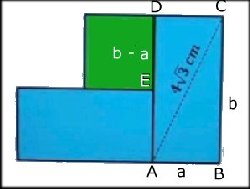 |
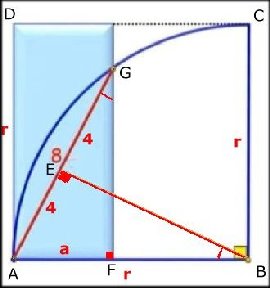
DEN BLÅ REKTANGELN
| Svar: 32
cm2 Lösning: Rektangelns area är a.r cm2 Triangeln ABE är likformig med triangeln AFG. AB/AG = AE/AF r/8 = 4/a a.r = 8 . 4 a.r = 32 (cm2) Tillbaka |
 |
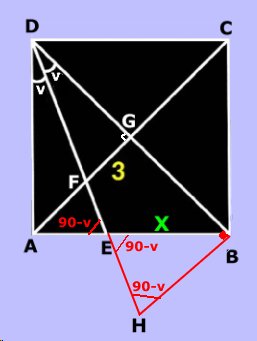
STRÄCKAN X
|
Svar:
Sträckan X är 6 cm. Lösning: Förläng sträckan DE så att vinkeln HBD blir rät. Kvadratens diagonaler bildar räta vinklar. Därför är triangeln DBH likformig med triangeln DGF. Eftersom DG = GB är alla sträckor i triangeln DBH dubbelt så stora som sträckorna i triangeln DGF. Sträckan BH är därför 6 cm. Av figuren framgår att den tredje vinkeln i trianglarna ADE och DBH är 90 - v. Vinkeln BEH = vinkeln AED (vertikalvinklar). Då är triangeln BEH likbent. Sträckan BE är därför lika med sträckan BH = 6 cm. |
 Tillbaka |
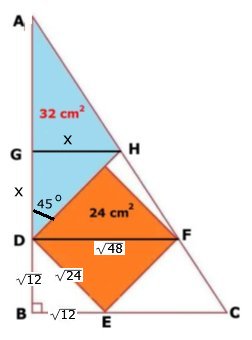
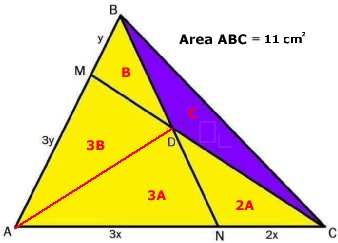
HUR STOR ÄR TRIANGELNS AREA?
|
Svar:
ABC:s area är 75 cm2. Lösning: Kvadratens area = (sidan)2. Då är DE = BD = Vinkeln GDH = 180o - 45o - 90o = 45o DG = GH = x (se figur). Den blå triangelns area = AD . GH/2 AD måste vara 64/x, eftersom 64/x . x/2 = 32. Triangeln AGH är likformig med ADF x/ Då är Triangeln ADF är likformig med ABC. Triangeln ABC:s area: BC . AB/2= 75 |
 Tillbaka |
|
REKTANGELNS AREA III |
|||
|
|||
|
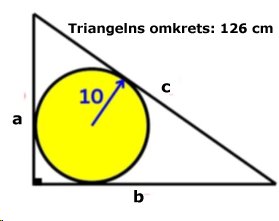
RÄTVINKLIG TRIANGEL |
|||
| Svar: Triangelns
sidor är 28 cm, 45 cm och 53 cm Lösning: Av tangenterna till cirkeln framgår att 2c + 2r = 126 2c + 20 = 126 c = 53 Då är a + b = 126 - 53 = 73 dvs. b = 73 - a Pythagoras sats ger: a2 + (73 - a)2 = 532 a2 + 5329 - 146a + a2 = 2809 2a2 - 146a + 2520 = 0 a2 - 73a + 1260 = 0 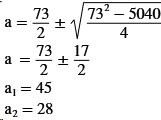
|
 |
||
|
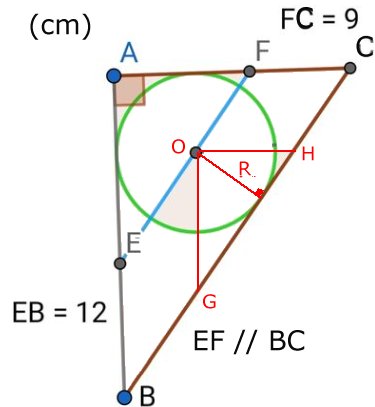
CIRKELNS RADIE |
|||
| Svar: Cirkelns
radie är 7,2 cm. Lösning: OG // BE och OH // FC OG = BE = 12 cm OH = FC = 9 cm Pythagoras sats på triangeln OGH ger: 122 + 92 = (GH)2 GH = 15 Arean på triangeln GHO ger ekvationen 15R/2 = 12 . 9/2 15R = 108 R = 7,2 |
 |
||
 cm
cm
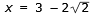 cm2
cm2