Månadens problem
september 2023 (lösning)

hälften så varmt 
Svar: Nej, lösningen är inte korrekt.
Lösning:
Man kan inte utgå från Fahrenheittermometern. Såväl Fahrenheittermometern som Celciustermometern har nollpunkter som är godtyckligt valda. På Celsiustermometern är
0 oC = vattnets fryspunkt och på Fahrenheitstermometern är 0 oF = den lägsta temperatur som man kunde uppnå när man blandade salt och is (1724), ca - 18 oC.

Det enda rimliga är att referera till den absoluta nollpunkten.
Då har molekyler och atomer sin lägsta rörelseenergi: Temperaturen är därför ett mått på dessa partiklars rörelseenergi.
0 K = - 273,15 °C.
0 °C är 273,15 K.
Hälften så varmt som 0 °C ligger alltså vid ≈ 136,6 K = -136,6 °C

Så låg temperatur har aldrig uppmätts i naturen. 
Den 24 augusti 1960 uppmätte ryska forskare - 88,3 oC vid Antarktis.
___

magneterna 
Svar: Det minsta antalet magneter är 30 st.
Lösning:
 Antag att det då är x st extra 8:or och y stycken extra 5:or.
Summan av 1 + 2 + 3... + 9 = 45
Summan av alla magneternas tal är 45 + 8x + 5y
Antalet magneter är  9 + x + y
Medelvärde:  (45 + 8x + 5y)/(9 + x + y) = 6,4
                   (450 + 80x + 50y)/(9 + x + y) = 64
Efter förenkling får man 16x - 14 y = 126
                                            8x = 63 + 7y
                                              x = 7(9 + y)/8
Minsta heltalsvärdet för x får man då y = 7
x =7(9 + 7)/8 = 7 . 16/8 = 14

Antalet magneter är
9 st (1, 2, 3, ...9) + 14 st (extra 8:or) + 7 st (extra 5:or) = 30 st
 

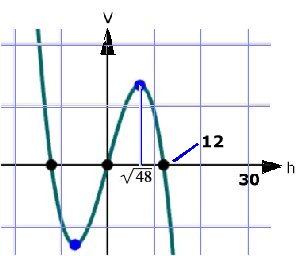
funktionen
Svar: g(648) = 43
Lösning:
g(a) + g(b) = g(ab)     g(2) = 5 och g(3) = 7   g(6) =12

g(648) = g(6) + g(108) = g(6) + g(6) + g(18) = g(6) + g(6) + g(6) + g(3) = 3g(6) + g(3) = 3 . 12 + 7 = 43
___

cylindern och klotet
Svar:
Förhållandet mellan klotets och cylinderns volymer är
Lösning:
Pythagoras sats ger:
r2 + (h/2)2  = 62     
r2 = 36 - h2/4     (1)

Cylinderns volym: r2 . h
V = (36 - h2/4) . . h
V = (36h - h3/4)
Derivera:
V ' (h) = (36 - 3h2/4)
V ' (h) = 0=>(36 - 3h2/4) = 0
h2 = 48
h = (endast den positiva roten är aktuell)
Med teckenstudium kan man visa att h = ger ett max.värde för cylinderns volym, men jag väljer en annan metod:
Av funktionen nedan framgår att cylindern har maximal volym när h=




h= insatt i ekv. (1) ger:
r2 = 36 - 48/4
r =



Extrauppgift:
Svar: Minimivärdet för cylindern, dvs. V = 0 inträffar när h = 0 och h = 12 (se funktionen till vänster)

När höjden är 12, är höjden = diametern i klotet. Det medför att cylinderns radie = 0.
 

kulorna
Svar: 10/21
Lösning:
Vi vet att kula nr 1 är röd och kula nr 3 är blå.

A.  R ___ B ___ ___ ___ ___ ___ ___

På hur många sätt kan de sju tomma fälten fyllas med 2 röda och  5 blå kulor?
Svar: Formeln ger svaret.

B.  R ___ B ___ ___ ___ ___ B B

 På hur många sätt kan de 5 tomma fälten fyllas med 2 röda och  3 blå kulor?
Svar: Formeln ger svaret.

Slutsats: 10 av 21 sekvenser slutar med två B, så sannolikheten att de två sista kulorna är blå är 10/21.
___

 Tillbaka