Månadens problem september 2022

Månadens problem
september 2022 (lösning)

varvtid

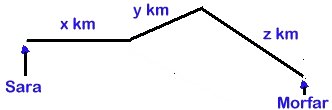
Uppg. 1:

Svar: Rasmus springer ett varv på 42 sekunder.
Lösning:
Alt. 1:
På 24 sekunder springer Lukas 24/56 = 3/7 av ett varv.
Det innebär Rasmus på 24 sekunder springer 4/7 av ett varv. Ett varv för Rasmus tar då 7 ^. 24/4 s = 42 s
Alt. 2:
Antag att Lukas hastighet är x m/s och Rasmus hastighet y m/s.
Ett varv på den cirkulära bana kan beskrivas på två sätt.
1) 56x m (Lukas springer ett varv)
2) 24x + 24 y (Lukas och Rasmus springer en sträcka som sammanlagt motsvarar ett varv)
Ekv. 56x = 24x + 24y
y = 4x/3
Tiderna för ett varv är omvänt proportionella mot hastigheterna.
Rasmus varvtid är därför 3/4 av 56 s = 42 s

listorna

Uppg. 2:
Svar: 6 olika listor
Lösning:
Antag att talen är x, x + 3, x + 6, x + 9 och x + 12
x + 12 är en multipel av x, dvs. (x + 12)/ x är ett positivt heltal.
Eftersom x och (x + 12)/x = 1 + 12/x är positiva heltal, kan x anta värdena
1, 2, 3, 4, 6 och 12.
Det finns alltså sex olika listor.

benådad?

Uppg. 3:

Svar: Sannolikheten att Abdullah blir benådad är 1/8 (12,5 %) Lösning: Abdullah kan lägga två mynt samtidigt 0, 1 eller 2 gånger:
Två mynt ingen gång: 1, 1, 1, 1, 1 Två mynt 1 gång: 2, 1, 1, 1 2:an kan placeras på 4 ställen Två mynt 2 gånger: 2, 2, 1 1:an kan placeras på 3 ställen Sammanlagt: 8 alternativ	1 alternativ 4 alternativ 3 alternativ
Sannolikheten att Abdullah väljer rätt alternativ är 1/8

den okända sträckan

Uppg. 4:

Svar: DE är 8 cm
Lösning:
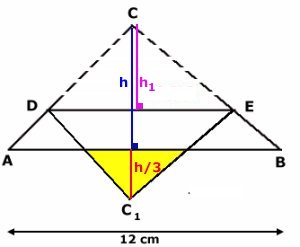
Antag att höjden i triangeln ABC är
h cm.
Antag att höjden från C resp. C₁ med DE som bas är h₁Triangeln DEC och den gula triangeln är likformiga med triangeln ABC.

Areaskalan = (längdskalan)².
Areaskalan när man jämför areorna av den gula triangeln och triangeln ABC är 1/9 enligt uppgiftens text.
Då är längskalan 1/3. Höjden i den gula triangeln är därför h/3.

Höjden h i triangel ABC mot sidan AB
= sträckan CC₁ - höjden (h/3) i den gula triangeln.
Det ger ekv.
2h₁ - h/3 = h
h₁= 2h/3
Då är sträckan DE =
2/3 av sträckan AB =
2/3 av 12 cm = 8 cm
(p.g.a. likformigheten)

bilresan

Uppg. 5:

Svar: Enkel resa är 308 km
Lösning:
Sträckorna vågrätt, uppför och nerför är markerade i figuren till höger.

Pelle P. och Staffan R. har skickat eleganta lösningar:
Pelle P.:s lösning:
Formeln för att räkna ut medelhastigheten om man först kör en sträcka med hastigheten v₁ och och sedan samma sträcka med hastigheten v₂ är

Bevis:

För sträckorna y och z i figuren kör Sara uppför åt ena hållet och nedför åt andra hållet.
Därför gäller formeln ovan för dessa sträckor:
v_m = 2 ^. 99 ^. 63/(99 + 63) = 77 (km/h)

Medelhastigheten för de kuperade sträckorna är alltså densamma som för den horisontella sträckan.
Totalt kör Sara fram och tillbaka i 3 h och 40 minuter + 4 h 20 minuter = 8 h
med medelhastigheten 77 km/h.
Enkel resa: 4 ^. 77 km = 308 km

Anm.: Uppgiften går att lösa, eftersom hastigheterna är valda så att medelhastigheten för de olika delarna (kuperade resp. horisontella) av resan blir lika stor.