Månadens problem
september 2020 (lösning)

 

Uppg. 1:
Svar: Entalssiffran i svaret är 5
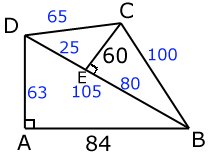
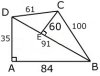
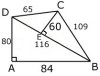
Figuren nedan visar en möjlig lösning.
  
Uppg. 2:
Svar: Rätt, om Wilma svarade 5!
         Fel, om Wilma svarade 5 (Multiplikation räknas före subtraktion)
Lösning:
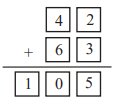
230 - 220 . 0,5 = 230 - 110 = 120
Wilma svarade 5!
5! betyder 1 . 2 . 3 . 4 . 5 = 120
Uppg. 3:
Svar: En tänkbar lösning är att AD är 63
och att BC är 100 och CD 65 (l.e.)
Lösning:
Det ligger nära till hands att undersöka om ABD är en egyptisk triangel, dvs. att förhållandet mellan sidorna är 3:4:5.
Om 84 motsvarar den längsta kateten, blir den kortaste kateten 3 . 84/4 = 63
Med Pytagoras sats får vi att BD är 105.
I triangeln BCE är CE = 60.
Är BCE också en egyptisk triangel?
Om CE är den kortaste kateten, skulle den längsta kateten vara 80 och sidan BC 100 (enligt Pythagoras sats).
Återstår att se om triangeln CDE får heltalssidor.
DE = 105 - 80 = 25
Med Pythagoras sats på triangeln CDE får vi att CD är 65 (En så kallad indisk triangel) och vi har därmed hittat en lösning.
 

Det finns ytterligare två lösningar:
 

Uppg. 4:
Bevis:
Ofta är det en fördel att göra symmetriska antaganden för att få enkla utryck med hjälp av konjugatregeln.
Låt oss därför kalla talen (x - 3/2), (x - 1/2), (x + 1/2), (x + 3/2)
(x - 3/2) . (x - 1/2) . (x + 1/2) . (x + 3/2) + 1 =
(x2 -  9/4) . (x2 - 1/4) + 1 =
x4 - 5x2/2 + 9/16 + 1 = x4 - 5x2/2 + 25/16 = x4 - 5x2/2 + (5/4)2 = (x2 - 5/4)2
Extrauppgift:
a) Svar: Produkten av fyra på varandra följande jämna heltal ökat med 16.
Bevis:
Vi kallar talen x -3, x - 1, x + 1, x + 3
(x - 3)(x - 1)(x + 1)(x + 3) = (x2 -  9)(x2 - 1) = x4 - 10x2 + 9
x4 - 10x2 + 9 an skrivas (x2)2 -2 . 5x2 + 9
Om siffertermen 9 ökas med 16 till 25 får man (x2)2 -2 . 5x2 + 25 = (x2 - 5)2
b) Svar: Produkten av fyra på varandra följande udda heltal ökat med 16
Beviset utförs på samma sätt som i a-uppg., men regeln gäller inte om ett udda antal av faktorerna är negativa.
 
Uppg. 5:
Svar:  k = 8/3
Lösning:
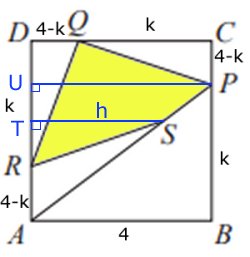
Arean av den gula fyrhörningen är lika med kvadratens area - arean av de fyra ursprung-
liga trianglarna.

Genom att  tillämpa likformighet på trianglarna  AST och APU får man reda på att höjden h i triangeln ARS är k.

Arean av
triangeln CPQ = triangeln DQR = k(4 - k)/2
triangeln ABP = 4k/2
triangeln ARS = k(4 - k)/2

Arean av fyrhörningen PQRS är
f(k) = 16 - 2 . k(4 - k)/2 - 4k/2 - k(4 - k)/2
f(k) = 16 - 4k + k2 - 2k -(4k - k2)/2

Derivera!
f ' (k) = -4 + 2k - 2 - 2 + k
f ' (k) = -8 + 3k
Sätt f ' (k) = 0
- 8 + 3k = 0
          k = 8/3
 

 

 

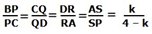
 Tillbaka