Månadens problem
september 2019 (lösning)
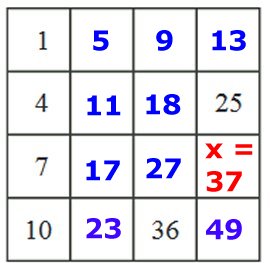
Uppg. 1:
a)
Svar: 37
b) Se figur till höger

 
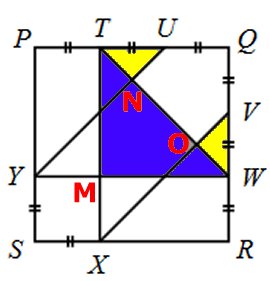
Uppg. 2:
Svar: 5/18
Lösning:
Antag att kvadratens sida är a (l.e.)
Triangel MTW
Basen är 2a/3 och höjden 2a/3
Arean: 4a2/18 (a.e.)

Arean av triangeln NTU =
arean av triangeln med OVW
basen är a/3 och höjden a/6 (höjden får man genom likformighet mellan trianglarna NTU och NWY)
Arean av båda trianglarna:
a2/18 (a.e.)
Hela skuggade arean:
4a2/18 + a2/18 = 5a2/18 (a.e.)		  

Uppg. 3:
Svar: x = 7 och y = 2
Lösning:
Eftersom y är ett heltal, är 8 - y2 ett heltal.
Då måste 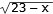också vara ett (positivt) heltal, dvs. 23 - x är en jämn kvadrat
Då vet vi också att 8 - y2 är ett positivt heltal.
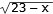är < 5
Vi behöver därför bara undersöka positiva y-värden, där 8 - y2 är < 5.
Enda tänkbara y-värdet är 2.
Insättning av y = 2 i det ursprungliga uttrycket ger x = 7
 
Uppg. 4:
Svar: När hypotenusan är en längdenhet större än den längsta kateten
Lösning:
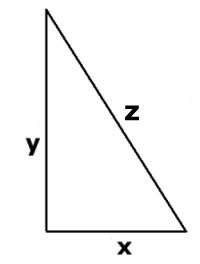
Antag att den längsta kateten är y och att hypotenusan är z.
Alt. 1: Pythagoras sats
x2 + y2 = z2
        x2  = z2 - y2      (1)

Alt. 2: Simons metod
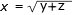   Kvadrera!
       x2  =  y + z        (2)

Jämför (1) och (2)
 z2 - y2 =  y + z
(z + y)(z - y) = y + z Dividera båda leden med y + z
            z - y = 1
                 z = y + 1
dvs. när hypotenusan är en längdenhet större än den längsta kateten.
 
Exempel på sådan pythagoreiska heltalstripplar är
3, 4, 5; 5, 12, 13; 7, 24, 25; 9, 40, 41; 11, 60, 61
Anm.: Om den minsta kateten (y) är ett udda tal >1, fungerar Simons metod när den längsta kateten är (y2 - 1)/2. (Hypotenusan blir (y2 + 1)/2)
 
Uppg. 5:
Svar: Cissi fyller år den 16 juli
Lösning:
Bland de tio alternativen förekommer 18 och 19 bara en gång.
Eftersom Bob inte direkt kan säga när Cissi har födelsedag, kan det inte vara 18 eller 19.
Om Cissi hade berättat för Adam att hon fyller år i maj eller juni, kunde hennes födelsedag varit 19 maj eller 18 juni. I så fall hade inte Adam kunnat säga att Bob inte visste. Då måste Cissi ha sagt till Adam att hon har födelsedag i juli eller augusti.
Av datum i juli och augusti är det bara 14 som förekommer två gånger.
Om Cissi hade sagt till Bob att hon fyller år den 14:e, hade Bob inte vetat när hon fyller år.
Nu återstår tre möjligheter: 16 juli, 15 augusti och 16 augusti.
Eftersom Adam nu kan säga när Cissi fyller år kan det inte vara i augusti (med två datum). Alltså måste det vara den 16 juli.		  

 

 Tillbaka