Månadens problem september 2018

Månadens problem
september 2018 (lösning)

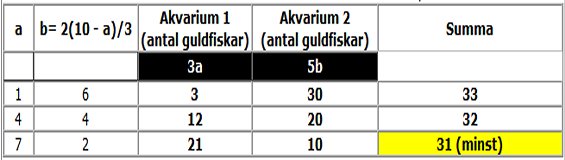
Uppg. 1:
Svar: 31 guldfiskar
Lösning:
Antag att det var 2a guppyfiskar och 3a guldfiskar i första akvariet.
3b guppyfiskar och 5b guldfiskar i andra akvariet.
Enligt texten är 2a + 3b = 20 (Rasmus har 20 guppyfiskar)
b = 2(10 - a)/3
Om täljaren i högra ledet ska vara delbar med 3, duger bara a-värdena 1, 4 och 7

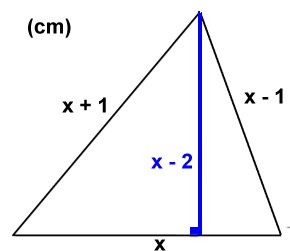
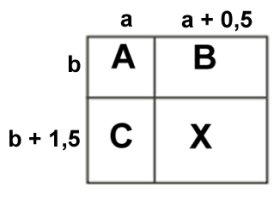
Uppg. 2:
Svar: 6 cm
Lösning:
Genom att jämföra omkretsarna av A, B och C får vi fram sträckorna a + 0,5 och b + 1,5

Omkretsen av X är
2(a + 0,5 + b + 1,5) = 2a + 2b + 4
Men 2a + 2b är omkretsen av A =
2 cm.
Alltså är omkretsen av X 6 cm.

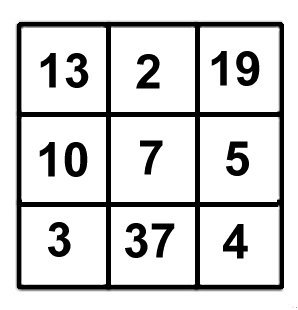
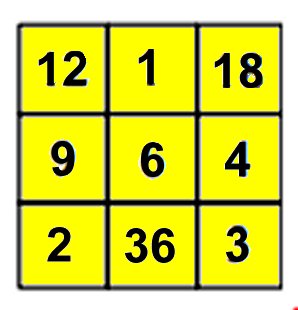
Uppg. 3:
Svar:
De ursprungliga talen finns i kvadraten till höger.
Bert har ökat alla tal med 1, så om vi minskar alla tal med 1 i Berts kvadrat, får vi fram de rätta talen.

För alla rader, kolumner och diagonaler gäller att produkten av de tre talen är 216.

Uppg. 4: Svar: 13, 14 och 15 cm Lösning: Antagande enligt figur. För att få en ekvation beräknar vi arean på två sätt. Alt.1: A = b^.h/2 A = x(x - 2)/2 Alt. 2: Använd Herons formel A =
Ekv.: x(x - 2)/2 = 1) Bryt ut x ur rotuttrycket och dividera båda leden med x. 2) Förenkla ekvationen och kvadrera sedan båda leden. 3) Efter förenkling får man x² - 16x + 28 = 0 4) När man löser andragradsekvationen får man x₁ = 14 x₂ = 2 (Duger inte. Höjden x - 2 blir 0) Sidorna är 13 cm, 14 cm och 15cm.