|
kuggad? |
|
Uppgifterna är hämtade från en
högstadietävling |
Ex. 1:
Svar:
15 varv
Lösning:
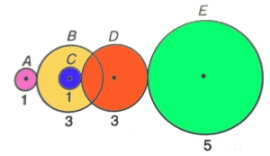
När man jämför två kugghjul blir antalet varv som de vrids
omvänt proportionellt till hjulens omkrets/ diameter.
När E vrids 1 varv, vrids D 5/3 varv.
När D vrids 5/3 varv, vrids C och B
5 varv. När B vrids 5 varv, vrids A
15 varv. |
 |
Ex. 2:
Svar:
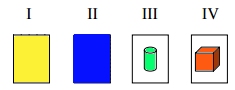
Kort I och III.
Lösning:
1) Vi kollar först om kort III verkligen har en blå baksida.
2) Baksidan kan vara blå även om det inte är en cylinder på
kortet! Därför behöver vi inte kolla det blå kortet. Vi
måste däremot kolla om det är en cylinder på det gula kortet
(kort I), för i så fall är ju inte påståendet sant. |
 |
Ex. 3:
Svar:
Omkretsen är 43 l.e.
Lösning:
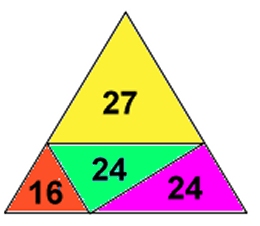
De sidor i den gula, röda och violetta triangeln som inte
ingår i den stora triangelns omkrets, motsvarar omkretsen i den
gröna triangeln.
Den stora triangelns omkrets är
27 + 16 + 24 - 24 = 43 (l.e.)
|
 |
Ex. 4:
Svar: 25
Lösning:
Eftersom alla heltal är olika, måste 45 delas upp i
fem faktorer på följande sätt:
1 . (-1) . 3 .
(-3) . 5
Det ger följande värden
a = 5, b = 7, c= 3, d = 9 och e = 1
a + b + c + d + e = 5 + 7 + 3 + 9 + 1 = 25 |
Talen a, b, c, d och e är alla
olika heltal sådana att
(6 − a)(6 − b)(6 − c)(6 − d)(6 − e) = 45
Vad blir a + b + c + d + e ? |
|