|
det var bättre förr!? Del 3 |
Efter
de deprimerande PISA-rapporterna är det intressant att se
svårighetsgraden på ett par
uppgifter från 1944: Övningsexempel i matematik för realgymnasiet,
R
I3 (Bengt Lindvall).
Den första uppgiften är något enklare, men den andra skulle nog
de flesta av dagens gymnasieelever få problem att lösa. |
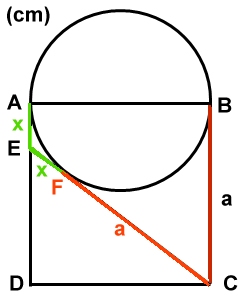
Ex. 1:
Svar:
Sidorna är 0,75a, a och 1,25 a
cm
Lösning:
Tangenterna CB = CF = a cm och
tangenterna EA = EF =x cm
Sidorna i triangeln CDE:
CD = a cm DE = (a - x) cm och
CE = (a + x) cm
Pytagoras sats på triangeln CDE ger:
a2 + (a - x)2 = (a + x)2
a2 + a2 - 2ax + x2 = a2
+ 2ax + x2
a2 = 4ax a> 0
a = 4x
x = 0,25a
DE = (a - 0,25a) cm = 0,75a cm
CD = a cm
CE = (a + 0,25a) cm = 1,25a cm |
 |
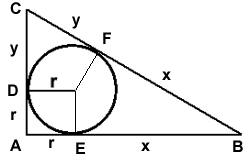
Ex. 2:
Svar: Sidorna
förhåller sig som 5:12:13
Lösning:
BE = BF = x (tangenter till cirkeln)
CD = CF = y (tangenter till cirkeln)
Pytagoras sats på triangeln ABC:
(r + x)2 + (r + y)2 = (x + y)2
Efter förenkling får vi
r2+2rx+x2+r2+2ry+y2
= x2 +2xy+y2
 (1)
(1)
Vi vet att cirkelns radie är 1/15 av av triangelns omkrets, dvs.
(r + x) + (r + y) + (x + y) = 15 r
2x + 2y + 2r = 15r
x + y = 6,5r (2)
(1) och (2) ger efter förenkling
y2 - 6,5ry + 7,5r2 = 0

Av figuren framgår att triangelns sidor är 2,5r, 6r och 6,5 r
Då förhåller sidorna sig som 5:12:13 |
 |
|