|
det var bättre förr!? Del 3 |
Efter
de deprimerande PISA-rapporterna är det intressant att se
svårighetsgraden på ett par
uppgifter från 1944: Övningsexempel i matematik för realgymnasiet,
R
I3 (Bengt Lindvall).
Den första uppgiften är något enklare, men den andra skulle nog
de flesta av dagens gymnasieelever få problem att lösa. |
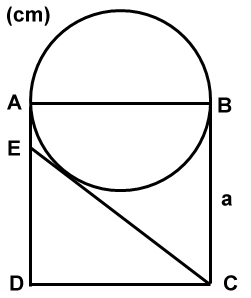
Ex. 1:
En kvadrat har sidan a cm. På
AB som diameter uppritas en cirkel. Från C drages en tangent
till cirkeln. Denna tangent dras ut och träffar sidan DA i E.
Bestäm sidornas längder i triangeln CED. |
 |
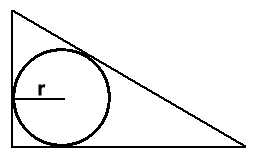
Ex. 2:
Hur förhåller sig en rätvinklig triangels sidor, om den
inskrivna cirkelns radie är 1/15 av av triangelns omkrets? |
 |
|