Cirkelresonemang

Två cirklars radie är 7 cm och 1 cm. Avståndet mellan deras medelpunkter är 10 cm. Beräkna längden av deras gemensamma tangenter.
(S.H. Persson: 20 träningsstilar för Realskolans högsta klass)
Svar: De yttre tangenterna är 8 cm och de inre tangenterna 6 cm.
Lösning:

Den yttre tangenten
Den yttre tangenten AB är lika lång som sträckan CD.
CD räknar du ut med Pytagoras sats på triangeln OCD.
CD = 8cm (egyptisk triangel

Den inre tangenten
Trianglarna ABC och CDE är likformiga.
Antag att sträckan CE är x cm. Då är sträckan AC (10 - x) cm.
Likformighet ger:
x/1 = (10 - x)/7   x = 5/4
Pytagoras sats på triangeln CDE: (CD)² + 1² = (5/4)²
Efter förenkling blir CD = 3/4 cm
Alla sträckor i triangeln ABC är 7 gånger så långa som motsvarande sträckor i triangeln CDE. Därför är sträckan BC = 7 ^. 3/4  cm = 21/4 cm
Den inre tangenten BD = 3/4 cm + 21/4 cm = 6 cm
 

Svar: Radien i den röda cirkeln är 8/9 cm

Lösning:

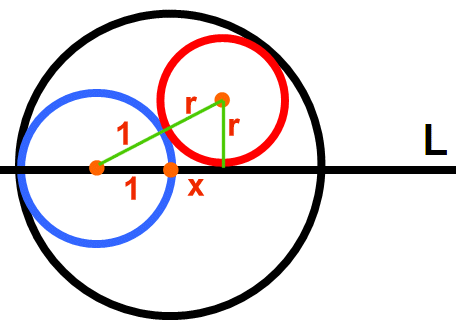
Pytagoras sats ger:
(x + 1)² + r²  = (r + 1)²
Efter förenkling får man
x² + 2x = 2r   (1)


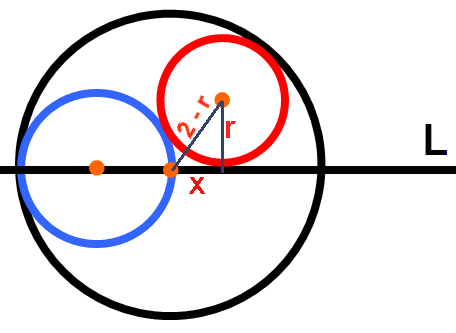
x² + r²  = (2 - r)²
Efter förenkling får man
x² + 2x = 2r
x² = 4 - 4r   (2)

Ekv. (1) och (2) bildar ett ekvationssystem
Vi multiplicerar båda leden i ekv. (1) med 2.
2x² + 4x = 4r   (3)

4r = 2x² + 4x insatt i ekv. (2) ger
x² = 4 - 2x² - 4x
3x² = - 4x + 4
x² = - 4x/3 + 4/3
  x₁ = 2/3
( x₂ = -2)

x= 2/3 insatt i ekv. (1) ger
4/9 + 12/9 = 2r 
         16/9 = 2r
              r = 8/9