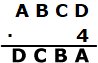|
sifferkoden |
Svar: 2178 . 4 = 8712
Lösning:
4 gånger
tusentalssiffran A och ev. minnessiffra ger
det ensiffriga talet D. Då kan A vara högst 2. A är
ett jämnt tal p.g.a multiplikationen 4
. D
(entalsraden). Därför är A = 2.
Då är D = 8 (tusentalsraden).
4
. A = D innnebar att 4
. B inte ger någon
minnessiffra. Då måste B = 1.

För att tiotalssiffran i svaret ska bli 1, måste
C = 7.
|
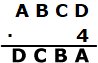
 |
|
|
triangeln |
Svar:
Sidorna är 20, 21 och 29 cm
Lösning:
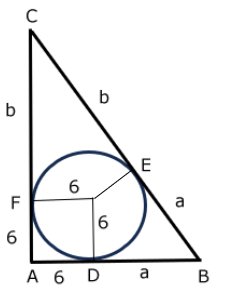
AD = AF = 6 cm
BD = BE = a cm
CE = CF = b cm
Två tangenter till cirkeln från en punkt utanför cirkeln är lika långa.
Cirkelns omkrets är 70 cm.
Ekv.: 2a + 2b + 2
. 6 = 70
a + b = 29
Hypotenusan BC är 29 cm.
Sidan AB + sidan AC = 70 cm - 29 cm = 41 cm (1)
|
 |
Alt 1: Fullständig andragradsekvation
Antag att AB är x cm och AC (41 - x) cm
Pythagoras sats ger
x2 + (41 - x)2 = 292
Formeln för andragradsekvationer ger efter förenkling:
x1
= 21 x2
= 20
Fall 1: AB = 21 cm AC = (41 - 21) cm = 20 cm
Fall 2: AB = 20 cm AC = (41 - 20 ) cm = 21 cm
dvs. två identiska lösningar
Alt. 2: Ofullständig andragradsekvation
Det gäller
att hitta ett antagande så att ekvationen inte innehåller både x2 och
x-termer
AB + AC = 41 enligt (1)
Antag att AC = 20,5 + x och AB = 20,5 - x (cm)
Problemet kan sedan lösas med Pythagoras sats eller med en ekvation, som
utgår från triangelns area. Då ser lösningen ut så här:
Triangelns area är
AB .
6/2 + BC .
6/2 + CA .
6/2 =
(AB +BC + CA)
.
6/2 cm2 =
70 . 6/2 cm2
= 210 cm2
Ekv.: (20, 5 + x)(20,5 - x)/2 = 210
420,25 - x2 = 420
x2 = 0,25
x1
= 0,5 x2
= - 0,5
Fall 1: AC = (20,5 + 0,5) cm = 21 cm
AB = (20,5 - 0,5) cm = 20 cm
Fall 2: AC = (20,5 +(-0,5)) cm = 20 cm
AB = (20,5 -(-0,5)) cm =
21 cm
dvs. två identiska lösningar.
|
|
|
|
bjudningen
|
Svar: På 241 920 sätt
Lösning: Värdinnan kan välja
bordskavaljer på 6
olika sätt.
Första damen bland gästerna kan välja
bordskavaljer på 8 sätt.
Andra damen kan välja
bordskavaljer på 7 sätt, tredje damen på 6 sätt osv.
Kombinationen av de gästande damernas valmöjligheter
är
8 . 7 . 6 . 5
. 4 . 3 . 2 .
1
Detta skriver man
8!
Kombinationen av
värdinnans och de gästande damernas valmöjligheter
blir 6
. 8!
= 241 920 |
|
|
|
|
|
|
|
likbenta trianglar |
Svar:
Vinkeln CDE = 20o
Lösning:
Triangeln ADE är likbent och vinklarna ADE
= AED = x.
Då är vinkeln DAE = 180 - 2x
(Vinkelsumman är 180o)
Vinkeln BAC =
40 + 180 - 2x
= 220 - 2x
Vinkeln B = Vinkeln C
=
(180 - (220 - 2x)) = x - 20
Antag att
vinkeln CDE = y
Enligt yttervinkelsatsen är då
x = x - 20 + y
y = 20
|
 |
|
Extrauppgift:
Svar: Man kan inte ange
den exakta storleken av vinklarna A, B och C. Det
framgår av att x = x - 20 + y (enligt
yttervinkelsatsen). Vid förenkling försvinner x,
dvs. x kan anta ett godtyckligt värde < 90o.
Dock kan man säga att vinkeln
A > 40o samt att vinkeln B = vinkeln C
och att var och en av dem är < 70o.
|
|
sista draget |
Svar: Aristoteles ska
inte börja.
Lösning: Aristoteles ska se till
att summan av de stenar som Platon och han
tar bort i en omgång är jämnt delbar med
10.
Ex.: Platon 1 sten, Aristoteles 9
stenar
Platon 4 stenar, Aristoteles 16 stenar
Platon 9 stenar, Aristoteles 1 sten
Platon 16 stenar, Aristoteles 4 stenar
Så
småningom finns det kvar 20 eller 10 stenar,
när Aristoteles har gjort sitt drag, och
hur
än Platon gör, kommer Aritoteles att vinna
efter ytterligare en eller två omgångar. |
|
|
|