Månadens problem
oktober 2021
Uppg. 1
En väska innehåller 40 bollar. Var och en av dem är antingen gul eller svart.
Maja tar slumpmässigt upp två bollar från väskan.
Sannolikheten för att båda bollarna är gula är 5/12.
Hur många gula bollar fanns ursprungligen i väskan?
Uppg. 2:

Talparen 
Antag att a = 5 och b = 4.
Bestäm alla heltalspar (K, L) med följande samband:
K2 + 3L2 = a2 + b2 − ab
 
Uppg. 3:

Sträckan cd 
I triangeln ABC är sträckan BC dubbelt så lång som sträckan AC.
Punkten D ligger utanför triangeln på linjen genom A och B, så att sträckan AD är en tredjedel av AB.
a) Beräkna förhållandet mellan sträckorna CD och AD. 
b) Vad kan man säga om vinkeln ACD?
 
Uppg. 4:

 inbromsningen 
En bilförare höll hastigheten 90 km/h.
När han var 100 m från en hastighetsbegränsning på 70 km/h, tryckte han på bromsen, eftersom han upptäckte en poliskontroll på 70-sträckan.
Det var mycket halt, så inbromsningen sker försiktigt. Hastigheten v(t) från inbromsningen till 70 km/h kan beräknas med formeln 25 . e-0,060t, där t är tiden i sekunder från inbromsningens början.
Hann bilföraren få ned hastigheten till 70 km/h, innan han var inne på 70-sträckan?
 

konen
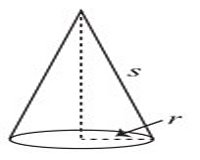
Uppg. 5:
En omålad kon har radien (r) 3 cm och generatrisen (s) 5 cm.
Konens basyta placeras i botten av en cirkulär behållare med färg. Färgdjupet i behållaren blir då 2 cm.
När konen sedan tas bort från cylindern, är basytan och den nedre delen av sidoytan täckt av färg.
Skriv förhållandet mellan den färgade arean och den totala arean som p/q, där p och q är positiva heltal, som inte kan förkortas.
Beräkna p + q.
Du kan mejla din lösning till mig (alf@mathpuzzle.se)
Pelle P. och Staffan R. har skickat lösningar.

 

 Lösningar  Tillbaka