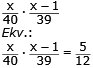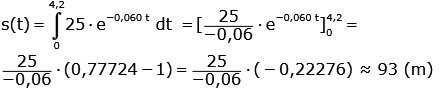Uppg. 1:
Svar:
26 gula bollar
Lösning:
Antag att det finns x gula bollar
Första bollen: Sannolikheten att bollen är
gul är x/40
Andra bollen: Sannolikheten att bollen är gul
är (x-1)/39
Sannolikheten att båda är gula är
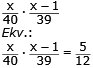
x2 - x = 650
x1 = 26
x2 = - 25 Duger inte. x > 0 |
|
|
|
Talparen |
Svar: (K, L)
har lösningarna (3, 2), (3, -2), (-3, 2), (-3, -2)
Lösning:
a = 5 och b = 4 => a2 + b2
− ab = 52 + 42 − 5 .
4 = 21, dvs. K2 + 3L2 =
21
L = 0 => K2 = 21, K är inte heltal
L = ± 1 => K2 = 18, K är inte
heltal
L = ± 2 => K2 = 9, K = ± 3
L = ± 3 => L32 = 27, K2 = -6
Det finns inga reella lösningar till K |
|
|
|
Sträckan cd |
a)
Svar: Förhållandet
CD:AD = 2:1
Bevis:
Enligt uppgiftstexten är BC:AC = 2:1
och AB:AD = 3:1.
Låt därför BC = 2x och AC = x samt
AB = 3y och AD = y
Cosinussatsen på triangeln ABC:
x2 = (2x)2 + (3y)2 - 2
. 2x . 3y .
cos v (1)
Cosinussatsen på triangeln BCD:
(CD)2 = (2x)2 + (4y)2 - 2
. 2x . 4y .
cos v (2)
x2 = 4x2 + 9y2 - 12xy
. cos v (1)
(CD)2 = 4x2 + 16y2 - 16xy
. cos v (2)
Vid lösning av ekvationssystemet är det
lämpligt att
eliminera xycos v. Turligt nog
kommer då även x2-termerna
att försvinna!
(CD)2 = 4y2
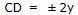
Endast den positiva roten duger
Då är CD:AD = 2:1
|
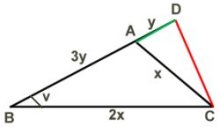
b)
Svar: Vinkeln ACD är lika stor som vinkeln B.
Motivering:
Första likformighetsfallet:
Om två sidor i en triangel är proportionella mot
två sidor i en annan triangel och mellanliggande vinklar är
lika stora, är trianglarna likformiga.
Detta gäller för trianglarna
CBD och ACD.
Då är vinkeln ACD lika stor som
vinkeln B.
|
|
|
|
|
inbromsningen |
Svar: Ja, han hade
sänkt hastigheten till 70 km/h efter ca 93 m.
Lösning:
Sträckan s(t) beräknas så här:
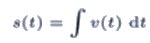
70 km/h = 70/3,6 m/s ≈ 19,44 m/s
Beräkna efter hur lång tid hastigheten har sjunkit till
19,44 m/s
19,44 = 25 . e-0,060t
19,44/25
= e-0,060t
Logaritmera båda leden
ln 19,44/25 = -0,06t . ln e
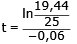
t
≈ 4,2 s
|
|
|
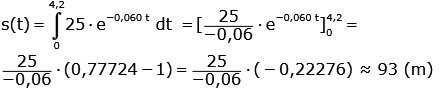
konen |
Uppg. 5:
Svar: p + q =
59 (p = 27 q = 32)
Lösning:
Enhet: cm
Basytan:
.
r2 = 9
Hela sidoytan enligt formeln
. r .
s
. 3 .
5 =15
s = generatrisen
q = 9
+ 15
= 24
Pyramidens höjd är 4 cm
(Pythagoras sats på triangeln ABC)
Färgdjupet är 2 cm.
|
 |
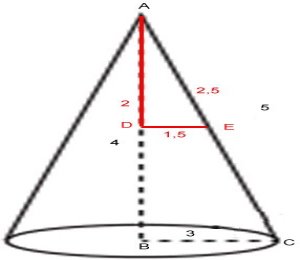Den del av konen som inte är målad har höjden (4 -
2) cm = 2 cm.
Triangeln ADE är likformig med triangeln ABC.
Då är DE = 1,5 cm och AE = 2,5 cm
Sidoytan som inte är målad:
. r .
s
=
. 1,5 .
2,5 = 3,75
p = 24
-3,75
= 20,25
p/q = 20,25/24
= 27/32
27/32 kan inte förkortas.
Då är
p + q = 27 + 32 = 59 |
|