|
Månadens
problem |
|
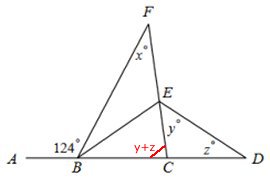
Uppg. 1: Svar: 124o Lösning: Vinkeln BCF är y + z enligt yttervinkel-satsen. Vinkeln ABF är x + y + z enligt yttervinkelsatsen. Alltså är x + y + z 124o. |
 |
|||||||||||||||||||||||||||||||
|
Uppg. 2: Svar: 7 värden Lösning: Det gäller att hitta de heltalsvärden som ger en jämn kvadrat under rotmärket. |
||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||
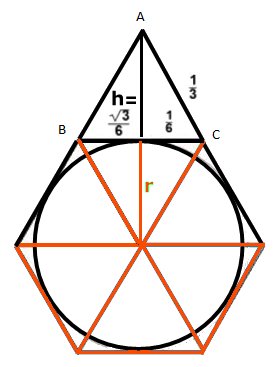
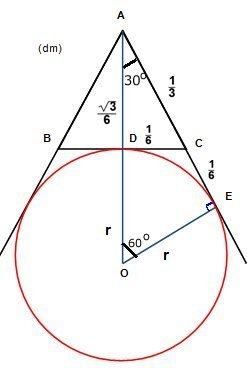
Uppg. 4:
Ett annat alternativ för
att beräkna radien: |
  |
|||||||||||||||||||||||||||||||
Uppg. 5:
|
||||||||||||||||||||||||||||||||