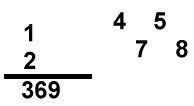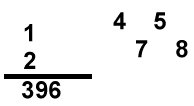Månadens problem
oktober 2018
Uppg. 1:
Svar: 4 lösningar
1) 0 tuppar, 25 höns, 75 kycklingar   (Denna lösning hade inte Liu Hui med.)
2) 4 tuppar, 18 höns, 78 kycklingar
3) 8 tuppar, 11 höns, 81 kycklingar
4) 12 tuppar, 4 höns, 84 kycklingar
Lösning:
Antag att man köper t tuppar, h hönor och  k kycklingar
Ekv.system:
t + h + k = 100
5t + 3h + k/3 = 100

Efter förenkling får man 7t + 4h = 100
För att få heltalslösningar inser man att t måste vara en multipel av 4.
t = 0 h = 25  k = 75
t = 4 h = 18  k = 78
t = 8 h = 11  k = 81
t = 12 h = 4  k = 84
 
Uppg. 2:
Svar: 5 cm2

Lösning:
Rektangeln är uppdelad i sex små trianglar.
Eftersom sträckorna AE, EF och FC är lika långa, är varje triangels area en sjättedel av rektangelns area.
Rektangelns area är 5 . 3 cm2 = 15 cm2
Fyrhörningen BFDE:s area är
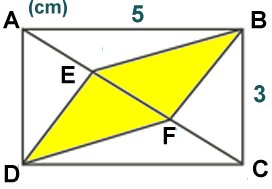
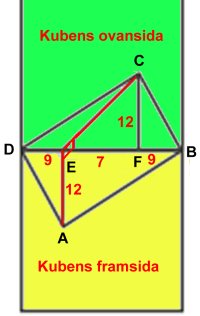
Uppg. 3:
a) Svar: 25 cm
Lösning:
Den kortaste vägen mellan A och C för myran om papperet ligger plant är diagonalen AC.
Det gäller även när papperet är vikt.
Diagonalen AC beräknas med Pythagoras sats till 25 cm.

b) Svar: cm ≈ 18,4 cm
Lösning:
Med likformighet får vi fram att AE = CF = 12 cm och
DE = BF = 9 cm.
AE är vinkelrät mot sträckan DB. Då är AE också vinkelrät mot CE.
Sträckan EF  = 25 cm - 9 cm - 9 cm = 7 cm.

Pythagoras sats på triangeln CEF ger
(CE)2 = 72 + 122   (CE)2 = 193 
Det kortaste avståndet från A till C får vi med Pythagoras sats:
(AC)2 = (AE)2 + (CE)2
(AC)2 = 144 + 193
(AC) =
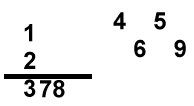
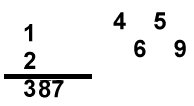
Uppg. 4:
a) Svar: Siffersumman i svaret ska vara 18.
Ett exempel är 314 + 658 = 972
Lösning:
Vi låter de tresiffriga talen betecknas så här:
abc (a är hundratalssiffra, b tiotalssiffra och c entalssiffra), def och ghi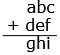

 

Tre fall är tänkbara:
1) Ingen minnessiffra
     Siffersumman 1 +2 + 3 + 4 + 5 +6 + 7 + 8 + 9 = 45
    I så fall är g + h + i = 45/2 = 22,5    Orimligt!
2) En minnessiffra
     I så fall är a + b + c + d + e + f = g + h + i + 9 (p.g.a. minnessiffran)
    45 + 9 = 54             54/2 är 27       g + h + i = 27 - 9 = 18
    Slutsats: Siffersumman i svaret är 18
3) Två minnessiffror
     I så fall är a + b + c + d + e + f = g + h + i + 18
    45 + 18 = 63   g + h + i + 18 = 63/2 = 31,5              Orimligt! 

b) Svar:  Hundratalssiffrorna 1,2 och 3 kan inte förekomma i det tredje talet.
Lösning:
Summan av två tal kan inte bli 1 eller 2, när varje siffra i siffrorna 1 - 9 bara får användas en gång.
Om hundratalssiffran i det tredje talet är 3, måste hundratalssiffrorna i de två första talen vara 1 och 2.
Följande alternativ återstår för det tredje talet, eftersom siffersumman ska vara 18:
378, 387, 369 och 396.
Vi tittar på om det går att placera in de återstående fyra siffrorna så att additionen stämmer:
1) 2)
3) 4)

Man inser lätt att det inte går att få additionerna att stämma.

Om hundratalssiffran i svaret är 4, 5, 6, 7, 8 eller 9 är det lätt att hitta exempel, där additionen stämmer.
 

Tillbaka