|
Nostalgitrippen
Uppgifter från en mattebok för åk 9, då
eleverna fortfarande hade bra resultat i Pisa-undersökningen
(Det var på 90-talet)
|
Ex.
1:
Svar:
a) 111 - 11 = 100
b) 3 . 33 + 3/3 = 100
c) 5 . 5 .
5 - 5 . 5 = 100
d) 7
. 7 +
7
. 7 +
7/7 + 7/7 = 100
e) 99 + 99/99 = 100
9
. 9 +
9 + 9 + 9/9 = 100
|
 |
Ex.
2:
Svar:
2,5 timmar
Lösning:
Pappa Göran klipper gräsmattan på 4 timmar. När han får
hjälp av sin hustru Sofia tar det bara halva tiden, 2 timmar.
Det betyder att de håller samma arbetstakt, dvs. Sofia skulle
ensam klippa gräsmattan på 4 timmar.
När Göran får hjälp av sonen Magnus tar det 2,5 timmar.
Eftersom Sofia klipper med samma hastighet som Göran, måste det
ta lika lång tid för Sofia och Magnus som för Göran och Magnus,
dvs. 2,5 timmar.
|
Ex. 3:
Svar:
Ja
Lösning:
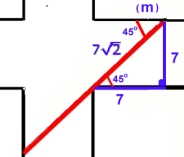
Av symmetriskäl inser man att det kritiska läget är när vinkeln v är 45o.
Den längd som flaggstången då högst kan ha är
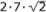 m
≈ 19,80 m, dvs. mer än den verkliga
flaggstångens längd. Vid andra vinklar är utrymmet större.
Det går att vika runt hörnet med flaggstången (men övriga
trafikanter uppskattar nog inte den här transporten). |
 |
|
|
|
Ex. 4:
Svar: Johanna har störst chans att vinna, om hon börjar
spela mot sin mamma.
Lösning:
Antag att sannolikheten för vinst mot mamman är m och
mot pappan är p.
Sannolikheten för förlust mot mamman och pappan är (1 - m)
resp. (1 - p)
Vinst två matcher i rad kan innebära att Johanna vinner alla
tre matcherna, eller de två första matcherna eller de två sista
matcherna.
Sannolikhet för vinst i minst två matcher
Alternativ 1:
Johanna börjar att spela mot mamman
mpm + mp(1-m) + (1-m)pm = mp(2 - m) (1)
Alternativ 2:
Johanna börjar att spela mot pappan
pmp + pm(1-p) + (1-p)mp = mp(2 - p)
(2)
Jämför (1) och (2)
Eftersom p > m är (2 - m) > (2 - p).
Därför ger alternativ 1 störst chans att vinna två gånger i rad.
Extrauppgift:
Svar:
Ja
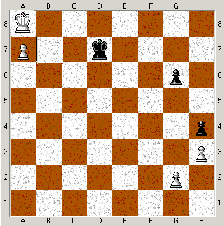
Lösning:
1. Svart spelar Kc8 eller Kc7
Vit är då i dragtvång, eftersom den vita kungen inte kan
flytta.
2. g2-g3, h4xg3 (eller 2. g2-g4, h4xg3 e.p.)
Svart vinner. |
 |
|
|