Svar: Barnen är 12 och 4
år.
Lösning:
Antag att barnen är x och y år.
Ekv.:
xy = 3(x + y)
xy = 3x + 3y
x(y -3) = 3y Skriv om högra ledet för att 3y - 9 ska kunna
delas med y - 3
x(y - 3) = 3y - 9 + 9
Dividera båda leden med (y - 3)
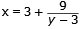
Vi förutsätter att barnens ålder anges som heltal.
y kan då anta följande värden:
y = 4 ger x = 12
y = 6 ger x = 6
y = 12 ger x = 4
Ekvationen ger alltså två lösningar: 4 år och 12 år eller
tvillingar, som är 6 år.
När magister Rask säger att det äldsta barnet är fött i
Lejonets stjärntecken, förstår Stella att magister Rask inte
har tvillingar.
|
|
|
Svar: 32o
Lösning:
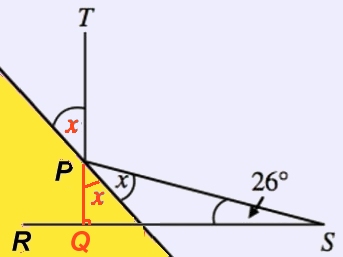
De röda vinklarna x är lika stora (vertikalvinklar)
Vinkelsumman i triangeln PQS ger ekvationen
2x + 90 + 26 = 180
x = 32 |
 |
|
|
Svar:
Parallelltrapetsets sidor är
AB = 5 l.e.
BC = CD = DA = 4 l.e.
Lösning:
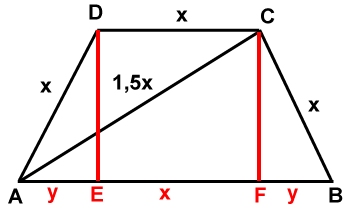
Sträckan AE = sträckan FB = y
Sträckan EF = sträckan DC = x
(CF)2 = x2 - y2
(Enligt Pytagoras sats på triangeln BCF)
(x + y)2 + x2 - y2 = (1,5x)2
(Enligt Pytagoras sats på triangeln AFC) |
 |
x2 + 2xy + y2
+ x2 - y2 = 2,25 x2
2xy = 0,25 x2
x ≠ 0
Dividera i båda leden med 2x
y = 0,125 x
y = 1/8 x
y = 1 och x = 8 ger heltalssidor, men det finns ett ännu mindre
alternativ, eftersom den längsta sidan är x +
2y
Därför duger x = 4 och y = 0,5
I det minsta parallelltrapetset med heltalssidor är x = 4 l.e.
och y = 0,5 l.e.
Parallelltrapetsets sidor är då
AB = 5 l.e.
BC = CD = DA = 4 l.e. |
|