|
halvcirklarna
|
Svar:
Radien(r)
är
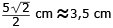
Lösning:
OA = OB = 5 cm (radier i den stora halvcirkeln.)
Vinkeln
AOB är 90o ( randvinkel i den lilla
halvcirkeln.)
Pythagoras sats ger:
52 + 52
= (2r)2
50 = 4r2
r =
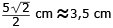 |
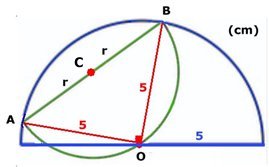
Anm:
Man kan
också beräkna r genom Pythagoras sats på triangeln ACO
(Vinkeln ACO är rät). |
|
|
|
|
tågen
|
Svar:
Avståndet mellan A och B är 400 km.
Lösning:
Antag att sträckan AB är x km.
s = v . t |
Tåget
från A:
s= 0,5 x km
v = 8 . 60/7 km/h = 480/7 km/h
t = s/v = 0,5 x/(480/7) h = 3,5x/480 h |
Tåget
från B:
s= 0,5 x km
v = 10 . 60/8 km/h = 75 km/h
t = s/v = 0,5 x/75 h |
Jämför tiderna!
Tiden för tåget från A är 15 min = 1/4 h längre än
tiden för tåget från B.
Ekv.: 3,5 x/480 = 0,5x/75 + 1/4 Mgn:
2400
17,5 x = 16x + 600
1,5x = 600
x = 400
|
|
bollarna |
Svar:
Sannolikheten för att det finns åtminstone
en grön boll och åtminstone en röd boll på
bordet, är 1 - 3/7 = 4/7
Lösning:
Om det finns åtminstone en grön boll och
åtminstone en röd boll på bordet, innebär
det att de två första bollarna inte hade
samma färg.
Sannolikheten för att de två första bollarna
är gröna är 3/7
.
2/6 = 1/7 och att de är röda är 4/7
.
3/6 = 2/7
Sannolikheten för att de två första bollarna
har samma färg: 1/7 + 2/7 = 3/7
Sannolikheten för att de båda första
bollarna inte har samma färg, dvs.att det
finns åtminstone en grön boll och åtminstone
en röd boll på bordet, är 1 - 3/7 = 4/7 |
|
|
|
|
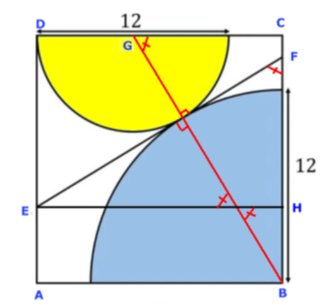
Sträckan EF |
Svar:
a) Kvadratens sida är
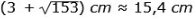
b) Sträckan EF är 18 cm
Lösning:
a) Sträckan BG är (12 + 6) cm = 18 cm
Antag att kvadratens sida är x cm.
Då är sträckan CG
= (x - 6) cm.
Pythagoras sats på triangeln BCG ger:
x2
+ (x - 6)2 = 182
Efter förenkling
blir det positiva x-värdet
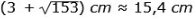
b) De vinklar som är markerade med
 är lika
stora. är lika
stora.
Då kan man dra slutsatsen att trianglarna BCG och
EFH är likformiga. Eftersom EH = BC är de också kongruenta.
Då är EF = BG = 18 cm. |
 |
| |
|
|
vinnande
strategi |
a)
Svar: Hugo har en vinnande strategi.
Lösning:
Hugo tar hela tiden bort lika många stenar som
Eilias, men från motsatt hög!
b)
Svar: Elias har en vinnande strategi.
Lösning:
Elias börjar med att ta bort en sten ur högen
med 40 stenar. Då
befinner sig Hugo i samma situation som Elias
gjorde, när spelet började i uppgift a.
Därför är det Elias som nu har den vinnande
strategin: Han tar i fortsättningen bort lika många
stenar som Hugo, men från motsatt hög. |
|

