|
Månadens
problem |
|
talmysteriet |
|||||
|
Svar: De romerska talen IV, IX, XL ... blir större när man tar bort siffran längst till vänster. |
|||||
|
litermåttet |
|||||
|
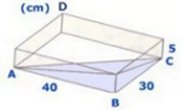
Lösning:
Fyll lådan till brädden med vatten och
ställ den på diskbänken. Lyft långsamt och försiktigt lådan i hörnet D så att hörnet B hela tiden vilar mot diskbänken. När så mycket vatten runnit ut, att halva botten ovanför diagonalen AC är fri från vatten, finns det kvar 1 liter vatten i lådan. |
 |
||||
|
Bevis: Vattnet bildar rymdfiguren ABC = en
pyramid. Basytan (A) är 40 . 30/2 cm2 = 600 cm2 Formel för pyramidens volym: A . h/3 V = 600 . 5/3 cm3 = 1000 cm3 = 1000 ml = 1 liter Alternativ lösning: Staffan R.: "Luta den vattenfyllda lådan t.ex. utefter kanten 40 cm så att 2/3 av lådans bottenyta torrläggs. Då återstår vattenvolymen 10 . 5 . 0,5 . 40 cm3 = 1 l. Jag förutsätter att längdmått finns." |
|||||
|
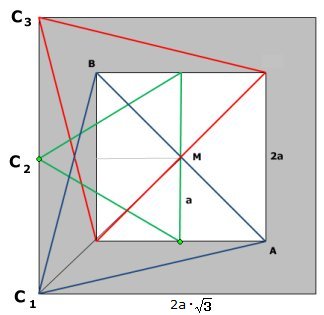
läget av hörnet c |
|||||
|
|||||
|
Då A rör sig på en av kvadratens horisontella sidor
är därför MC:s horisontella projektion konstant a Härav följer att de möjliga lägena för C bildar en ny kvadrat med medelpunkt i M, med sidlängden 2a . Alternativa lösningar Staffan R. har lagt in kvadraten i ett koordinatsystem med kvadratens mittpunkt i origo och sedan visat att alla möjliga lägen för C bildar en kvadrat med medelpunkten i origo och med sidan 2a . Pelle P. har på liknande sätt lagt in kvadraten i ett koordinatsystem med kvadratens mittpunkt i origo men sedan använt det imaginära talplanet. |
|||||
|
hamstrar och papegojor |
|||||
|
|||||
|
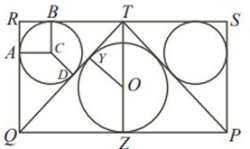
Rektangeln |
|||||
|
|||||