Uppg. 1:
Svar: 225
Lösning:
Antag att antalet små kvadrater är a2
Antal skuggade kvadrater är 2a - 1 (-1
eftersom mittenrutan är räknad 2 ggr)
Antal vita kvadrater: a2 -
(2a - 1) = a2 - 2a + 1
Ekvation: a2 - 2a + 1 = 196
Lös denna
andragradsekvation!
a1= 15
(a2= - 13)
Antalet små kvadrater: 152 =
225
|
Uppg.
2:
Svar:
Lösning: |
|
a)
Svar: 4 1/8 h = 4 h 7,5 min
Lösning:
Med motorcykel tar det 135/90 h =
1,5 h att köra till orten X.
C har då gått 1,5 .
6 km = 9 km.
När A vänder om för att möta C är sträckan
(135 - 9) km = 126 km och den sammanlagda hastigheten (90 +
6) km/h = 96 km/h.
A och C möts efter 126/96 h = 21/16 h
Vägen tillbaka till X tar också 21/16 h.
Total tid:1,5 h + 2 . 21/16 h = 4 1/8 h
b)
Svar: 3 h 50 min |
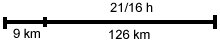
 |
|
Lösning:
Av "symmetriskäl" inser man att alla tre kommer till
orten X snabbast, om B och C går lika långa sträckor (x km i
fig. 2) och åker motorcykel lika långa sträckor
(135 - x km i fig. 2)
A kör och B åker med på motorcykeln till
punkten 1 och B går sedan till orten X.
A vänder om och möter C i punkten 2. Därefter åker A och C
till X.
När A möter C, har
A kört
(135 - x) + (135 - 2x) = 270 - 3x (km)
Tid: (270 - 3x)/90
(1)
Under samma tid har C gått x km.
Tid: x/6
(2)
Ekv.: (270 - 3x)/90 = x/6
x = 15
Den sammanlagda tiden kan skrivas som tiden
C går + tiden med
A+C på mc:n.
Sammanlagd tid (h): x/6 +
(135 -x)/90
x = 15 =>
Total tid: (15/6 + 120/90) h = 3 h 50 min
Av fig. 2 framgår att B och C går lika långa sträckor (x km)
och åker motorcykel lika långa sträckor (135 - x km). Därför
kommer A, B och C samtidigt till orten X.
|
|
|
Uppg. 3:
Svar:
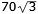 cm3 ≈
121
cm3 cm3 ≈
121
cm3
Lösning:
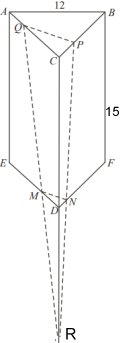
Om sträckorna QM, CD, PN förlängs, kommer de att
skära varandra i en punkt (R). Man får då en pyramid
med CPQ som basyta.
Denna pyramid är likformig med pyramiden med DMN som
basyta och spetsen i punkten R. Längdskalan är 2:1
Då är volymskalan 23:1 = 8:1.
Volymen av QPCDMN är därför 7/8 av volymen av
pyramiden CPQR.
CQ = 8 cm. Då är CP = 4 cm och PQ =
 cm. cm.
Pyramiden CPQR:s basyta = 4 .
 /2
cm2 /2
cm2
Pyramiden CPQR:s höjd = 2 .
15 cm = 30 cm
Pyramiden CPQR:s volym:
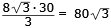 cm3
cm3
|
 |
|
Uppg.
4
Svar: Siffersumman är 11
Lösning: |
2k . 5300
Om k = 300 kan 2k . 5300
skrivas 2300 . 5300 (2 .
5)300
= 10300
Talet 10300
består en etta och 300 st. nollor.
För att få ett tal med 303 siffror måste
10300
multipliceras med ett tresiffrigt tal.
Det minsta värde som 2 kan upphöjas till för att
få ett tresiffrigt tal är 7.
27=
128 Då är k = 300 + 7 = 307
2307 . 5300
= 27
. 10300
= 128
. 10300
Siffersumman är då 1 + 2 + 8 + 0 + ..... + 0
(300 st nollor) = 11
|
|
Uppg. 5 |
|
Svar:
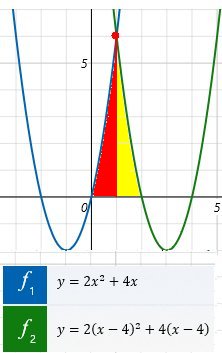
Emma ritade först grafen till y = 2x2 + 4x |
Lösning:
a)
Låt den första funktionen vara f(x)1= ax2
+ bx
Den parallellförskjutna funktionen, 4 steg åt höger, får
man genom att ersätta x med (x - 4)
f(x)2 = a(x - 4)2 + b(x - 4)
Skärningspunkten ger ekvationen
ax2 + bx = a(x - 4)2 + b(x - 4)
Vi vet att skärningspunkten har x-värdet 1.
a + b = a(1 - 4)2 + b(1 - 4)
a + b = 9a - 3b
4b = 8a
b = 2a (1)
Skärningspunkten har y-värdet 6, dvs.
ax2 + bx = 6 men x = 1 och b = 2a
enligt (1)
a + 2a = 6
a = 2 då är b = 2a
= 4
Emma ritade först grafen till y = 2x2 + 4x.
Anm.: Om grafen flyttas 4 steg
åt vänster ersätter
man x med (x + 4). |
 |
b)
Svar: 16/3 a.e.
Lösning:
I figuren är x = 1 symmetrilinje till arean,
dvs. den röda och gula arean är lika stora.
Den röda arean:
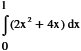 =
=
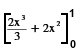 =
8/3 =
8/3
Hela arean = 2 . 8/3 = 16/3 (a.e.) |
|
|