Uppg. 1:
Svar: 1,1 m
Lösning:
Alt.1:
Längden av 10 kundvagnar är 2,9 m och längden av
20 kundvagnar är 4,9 m.
Längden ökas alltså med (4,9 - 2,9) m = 2 m för
ytterligare 10 vagnar.
För varje vagn blir ökningen då 0,2 m.
Om vi från raden med 10 kundvagnar tar bort 9
kundvagnar, blir längden av den återstående
vagnen 2,9 m - 9 . 0,2 m = 1,1
m
Alt. 2:
När man skjuter in en kundvagn under den
framförvarande kundvagnen, kommer större delen
av kundvagnen att hamna under den framförvarande
kundvagnen.
Med ett ekvationssystem kan man beräkna delen
utanför resp. under den framförvarande
kundvagnen.
|
Uppg.
2:
Svar:
3 400 m
Lösning: |
|
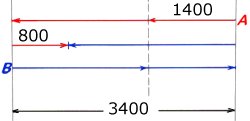
Se figur:
När färjorna möts första gången, har de
tillsammans avverkat avståndet mellan
färjestationerna. A har då kört 1400 m.
När de möts andra gången är den sam-manlagda
sträckan = tre gånger avståndet mellan
färjestationerna.
Färja A har då kört 3 .
1400 m = 4200 m
Av figuren framgår att A har kört hela avståndet
mellan stationerna + 800 m.
Avståndet mellan stationerna är:
4200 m - 800 m = 3400 m.
|
 |
|
|
Uppg. 3
Svar: Sannolikheten för att Patrik och
Viktor hamnar vid samma bord är 2/7.
Lösning:
Antag att de 15 eleverna får dra var sin
lapp, där det står vid vilket bord eleven ska
sitta. Om Viktor ska hamna vid samma bord som
Patrik, återstår det fyra av sammanlagt 14
platser.
Sannolikheten är 4/14 = 2/7.
|
|
|
Uppg.
4 |
|
 |
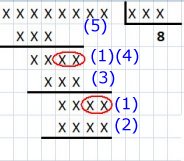
Lösning:
Kvoten
När två siffror flyttas (1) ner istället för en måste
det finnas en nolla i kvoten.
Kvoten kan därför skrivas X080X.
När divisorn (nämnaren) multipliceras med den femte
siffran i kvoten blir produkten ett fyrsiffrigt tal.
(2)
Kvotens femte siffra måste då vara en nia, eftersom 8
gånger divisorn ger en tresiffrig produkt.
(3)
Divisorn (nämnaren) måste vara mindre än 125, eftersom 8 gånger
divisorn ger en tresiffrig produkt.
(3)
Första siffran i kvoten kan inte vara en sjua, för då
skulle den första subtraktionen ge ett tresiffrigt tal.
(4)
Förstasiffran är därför en åtta.
Divisorn (nämnaren)
Divisorn kan inte vara 123 (eller 125 enligt tidigare
resonemang), eftersom
123 . 80809 ger
en sjusiffrig produkt och dividenden (täljaren) i det
här problemet har åtta siffror.
(5)
Divisorn är därför 124.
Dividenden (täljaren)
Slutligen beräknar vi dividenden som produkten av 80809
. 124 = 10020316
|
|
Uppg. 5 |
 |
 |
Svar: Ja, rören räcker.
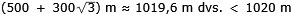
Lösning:
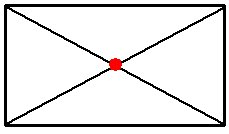
Det ligger nära till hands att undersöka en
symmetrisk lösning, dvs. att brunnen ligger
diagonalernas skärningspunkt.
● Men om rören följer diagonalerna blir den
totala röråtgången ca 1166 m.
● Det gäller därför att hitta en lösning, där
två hus delvis har ett gemensamt rör.
I figuren till höger är M mittpunkt och
EM = 250 -x gemensam ledning för A och B.
Rörledning för A och B:
f(x) =
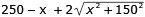
Bestäm funktonens minsta värde genom att
derivera och sedan sätta f '(x) = 0
f '(x) =
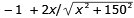
f '(x) = 0 ger
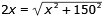
Kvadrera båda leden!
4x2 = x2 + 1502
Den positiva roten till denna
andra-gradsekvation är
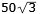
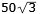 insatt
i
f(x) = insatt
i
f(x) =
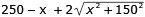 ger
f(x) =
ger
f(x) =
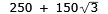
Röråtgången för alla fyra husen:
2(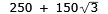 )
m ≈ 1019,6 m )
m ≈ 1019,6 m |
|
|