Uppg. 1:
Svar: 40 lösningar
Lösning:
Värdet av ABC är 100A + 10B + C och värdet av
CBA är 100C + 10 B +A
Ekv.: 100A
+ 10B + C - 100C - 10 B -A = 495
99(A - C) = 495
A - C = 5
C ≠
0, eftersom CBA är
ett tresiffrigt tal.
A - C = 5 ger fyra
möjligheter:
6 - 1 = 5
7 - 2 = 5
8 - 3
= 5
9 - 4 = 5
Eftersom värdet av B inte
påverkar lösningen, kan B vara någon av
siffrorna
0 - 9. Det ger tio
möjligheter.
Antal lösningar: 4 .
10 = 40
|
Uppg.
2:
Svar: 21 cm
Lösning:
Om det inte går att bilda en triangel av
stickorna a, b och c, gäller att
a + b ≤
c
Den största stickan har sin minsta
längd när de åtta stickorna har följande
längder: 1 cm, 1 cm, 2 cm, 3 cm, 5 cm, 8
cm, 13 cm och 21 cm (Fibonacciserien).
|
|
|
|
| Uppg. 3
Svar: 2:5
Lösning:
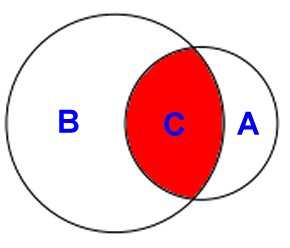
Antag att A är arean av hela den
lilla cirkeln, B är arean av hela den stora
cirkeln och C är den gemensamma arean.
Enligt uppgiften är C = 3/5 av A och 6/25 av
B.
Ekv.:
3A/5 = 6B/25
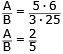
|
 |
|
Uppg.
4
a) Svar:
24 cm
Lösning:
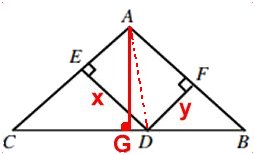
Antag att DE är
x cm och DF y cm.
Höjden AG mot sidan BC
beräknas med Pythagoras sats till 15 cm.
Jämför arean av ΔACD och ΔABD med arean av ΔABC
25x/2 + 25y/2 = 40 . 15/2
25(x + y) = 600
x + y = 24
b) Svar: Mitt på sidan
BC
Lösning:
Av symmetriskäl verkar
det troligt att arean av fyrhörningen AEDF är så
stor som möjligt när D ligger mitt på sidan BC.
En lösning kan se ut så här:
Trianglarna CDE
och BDF är likformiga med triangeln ACG i den
övre figuren.
Areaskalan = (längdskalan)2
Arean av triangeln ACG är 150 cm2
Fyrhörningens area (A) beräknas:
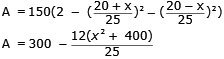
Extrauppgift:
Svar: 47,25 cm2
Lösning:
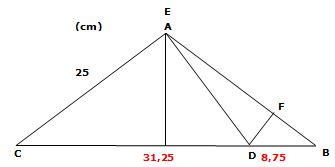
Gränsvärdet när AEDF inte längre är en
fyrhörning får vi när punkten E eller F
sammanfaller med A.
Med likformighet kan man då beräkna
CD till 31,25 cm.
På grund av symmetrin inser vi att AEDF är en
fyrhörning då
8,75 < CD < 31,25.
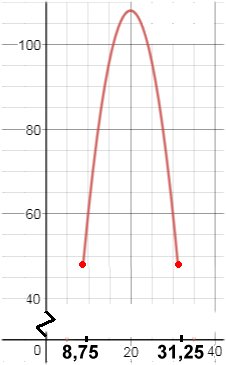
Andragradskurvan till funktionen för
fyrhörningens area är symmetrisk med ett
maxvärde (108 cm2) när D är mittpunkt
på BC.
Av andragradskurvan framgår det också att
fyrhörningen har sin minsta area vid
gränsvärdena 8,75 cm och 31,25 cm.
Vi beräknar arean av AEDF vid gränsvärdet CD =
31,25 cm
Areaskalan = (längdskalan)2
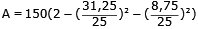
A = 47,25 cm2
|
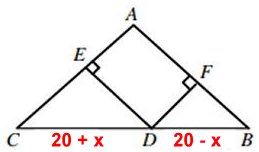
Vi inser att arean
av fyrhörningen AEDF är störst när x = 0, dvs.
när D är mittpunkt på sidan BC.
Arean av AEDF
är 108 cm2
|
|
|