Månadens problem november 2018

Uppg. 1:

ABC och CBA är två tresiffriga tal.
ABC - CBA = 495

Hur många lösningar finns det till ekvationen ovan?

Uppg. 2:
Lukas har åtta stickor. Längden på alla stickor i cm är naturliga tal.
Vilka tre stickor Lukas än tar, lyckas han inte bilda en triangel.
Vilket är den minsta längden som den längsta stickan kan ha?

Uppg. 3:

De två cirklarna täcker delvis varandra. Den gemensamma arean är 3/5 av den mindre cirkelns area och 6/25 av den större cirkelns area.
Vad är förhållandet mellan arean av den mindre cirkeln och arean av den större cirkeln.

Uppg. 4:

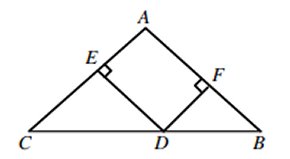
I den likbenta triangeln ABC är
AB = AC = 25 cm och BC 40 cm.
Från en godtycklig punkt D på sidan BC dras vinkelräta linjer (DE och DF) till AC resp. AB.
a) Vad är den sammanlagda längden av DE och DF?
b) Var på sidan BC är punkten D belägen för att arean av fyrhörningen AEDF ska bli så stor som möjligt?
Extrauppgift:
Vilket är det minsta värdet, som arean av fyrhörningen AEDF kan anta?