Uppg. 1:
Svar: 14
Lösning:
Om det sitter n fåglar på telefontråden finns det (n -
1) mellanrum.
105 motsvarar därför 2n - 1, där n är antalet fåglar innan de
sista fåglarna hade satt sig på telefontråden.
2n - 1 = 105 2n = 106 n = 53
Metoden för att finna antalet fåglar, när vi går ett steg tillbaka,
blir alltså att addera 1 till det nuvarande antalet och sedan
dividera med 2.
(3) 105
(2) (105 + 1)/2 = 53
(1) (53 + 1)/2 = 27
(Ursprungligt antal fåglar): (27 + 1)/2 = 14
|
entalssiffran |
Uppg. 2:
Svar: 0
Lösning:
(1720-1)17
1720 = (174)5
I talet 174 är entalssiffran 1
Då är entalssiffran i (174)5 = 1720
också 1.
Entalssiffran i
1720
- 1 är 0
Då är entalssiffran
i (1720 - 1)17
också 0.
|
|
läxproven |
Svar:
Tre läxprov med över 20 poäng, två läxprov med 20 poäng och
sju läxprov under 20 poäng.
Lösning:
Uppgiften kan lösas med ekvation, men man kan också resonera
sig fram till ett svar:
För varje prov över 20 poäng ligger resultatet i genomsnitt
7 poäng över medelvärdet, medan resultaten under 20 poäng i
genomsnitt ligger 3 poäng under medelvärdet.
För att det totala medelvärdet ska bli 20, dvs. att proven
över och under 20 poäng ska ta ut varandra, inser man att
det måste vara 3 prov över 20 poäng och 7 prov under 20
poäng. De två återstående proven måste då ha haft 20 poäng.
Anm.: 6 prov över 20 poäng och 14 prov under 20 poäng
skulle också ge medelvärdet 20 poäng, men det alternativet
duger inte, eftersom det var sammanlagt 12 prov.
|
|
Uppg. 4:
Lösning:
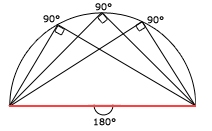
Enligt randvinkelsatsen är randvinkeln hälften så
stor som medelpunktsvinkeln på samma cirkelbåge.
När
cirkelbågen är en halvcirkel (180 grader) är randvinkeln
90 grader.
(se fig. nedan)
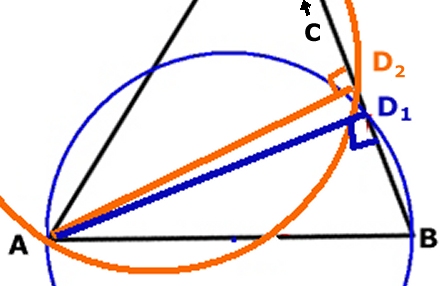
Vi gör först antagandet att de två cirklarna skär sidan BC i
två olika punkter D1 och D2.
Vinklarna AD1B
och
AD2C
är 90o enligt randvinkelsatsen. Det skulle i så
fall betyda att det från A går att rita två linjer (AD1
och
AD2)
vinkelrätt mot BC.
Orimligt!
D1
och
D2´måste
vara samma punkt. |
 |
|
|