Bisektriserna

Uppgift 1:

Svar: 2 cm²
Lösning:
Triangeln ADE är en halv kvadrat. Därför är vinkeln AED 90^o. Då är det lätt att visa att fyrhörningen  EFGH är en kvadrat.
Sträckan DJ = AD = 4 cm. Då är sträckan JC 6 cm - 4 cm = 2 cm. Därför är diagonalen i kvadraten  EFGH 2 cm.
Arean av en romb (med specialfallet kvadrat) är d₁^. d₂/2
A = 2 ^. 2 /2 cm² = 2 cm²

Bevis:
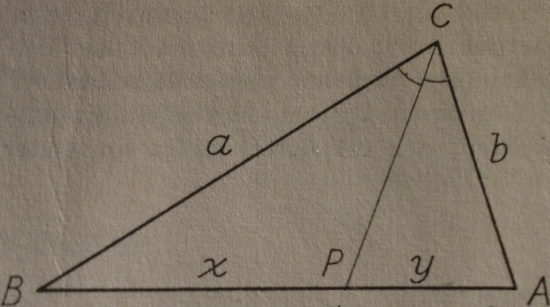
Enligt bisektrissatsen delar bisektrisen sidan AB i två delar, som förhåller sig som de övriga sidorna.
Med figurens beteckningar får vi x/y = a/b.


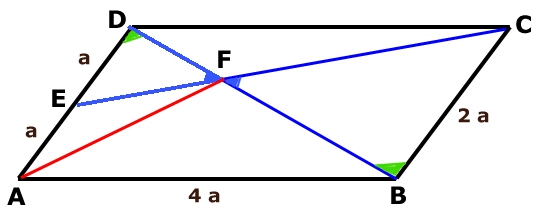
Om AF är en bisektris ska den dela sträckan DB i förhållandet 1:2 eftersom AD/AB = 1:2.
Det gäller alltså att bevisa att DF/FB = 1:2.
Triangeln DEF är likformig med triangeln BCF (likvinkliga trianglar).
Likformighet ger
DF/FB = DE/BC
DF/FB = a/2a
DF/FB = 1/2    V.S.B.