|
talet x |
Svar:
Talet x = 32
Lösning:
Ruta 3-5: Talet i ruta 3 är 52 - x
Ruta 2-4: Talet i ruta 2 är 78 - 2x
Ruta 1-3:
8 + 52 - x = 2(78 - 2x)
60 - x = 156 - 4x
3x = 96
x = 32
|
|
8 |
78 - 2x |
52 - x |
26 |
x |
|
1 |
2 |
3 |
4 |
5 |
|
|
|
aritmetisk
serie |
a)
Svar: Termerna är 3 och 12
Lösning: 36 kan delas upp i faktorerna 1.36,
2.18, 3.12, 4.9,
6.6
Endast 3 och 12 är symmetriskt belägna termer jämfört med -5
och 20.
b)
Svar: 26 termer
Lösning:
Differensen mellan - 5 och 3 är 8, differensen mellan 3 och
12 är 9 och differensen mellan 12 och 20 är 8.
Eftersom differensen mellan två på varandra följande termer
alltid är lika stor, är enda möjligheten att differensen är
1.
Då är antalet termer
-5 till -1: 5 termer
0: 1 term
1-20: 20 termer, dvs. sammanlagt 26 termer.
|
|
triangeln |
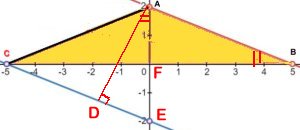
Svar: Arean
är 10 a.e. oberoende av var punkten C ligger på
linjen m.
Lösning: |
Om vi väljer
AB som bas i triangeln ABC, är höjden det
vinkelräta avståndet mellan de parallella
linjerna l
och m oberoende av var punkten C ligger på
linjen m.
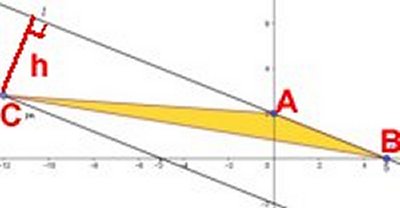
Om man istället väljer att placera punkten C i
skärningspunkten mellan linjen m och någon av
koordinataxlarna, får man en enklare lösning, där såväl bas
som höjd är heltal.:
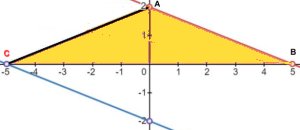
Alt. 1:
Flytta punkten C till den punkt, där linjen m skär
x-axeln (se figur nedan).
Låt CB vara bas = 10 l.e. Höjden är då 2 l.e.
Triangelns area är 10 . 2/2 a.e. = 10 a.e.
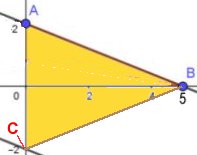
Alt. 2:
Flytta punkten C till den punkt, där linjen m skär
y-axeln (se figur nedan).
Låt AC vara bas = 4 l.e. Höjden är då 5 l.e.
Triangelns area är 4 . 5/2 a.e. = 10 a.e.
Ytterligare en lösning
(men inte alls lika elegant!)
Triangeln ADE är likformig med triangeln ABF.
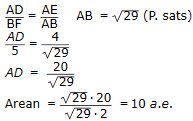
|
 |
|
|
Bollarna |
Svar: 66 olika sätt
Lösning:
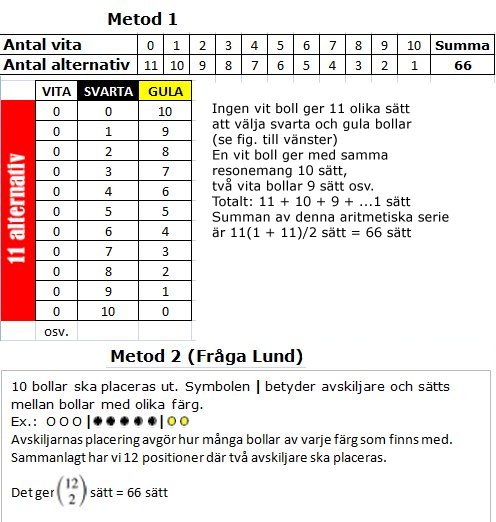 |
|
tetraedern |
Svar: a) Punkten P ligger i hörnet A
b) Volymen är 72 cm3
Lösning:
I kvadraten till vänster är
CE = CF =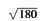 cm cm
Triangeln ACE i pyramiden till höger
är rätvinklig, eftersom
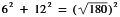
a)
Då är AC är höjd i pyramiden.
Punkten P ligger i hörnet A, sedan
kvadraten vikts till en tetraeder.
b)
Volymen =
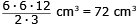 |
 |
Godtycklig sidlängd:
Kvadratens sida är a
V = a3/24 |
|