Svar: 28
Lösning:
Alt. 1:
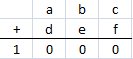
Välj godtyckliga värden på a, b och c och
sedan värden så att abc + def = 1000
Ex.: 279 + 721 = 1000
2 + 7 + 9 + 7 + 2 + 1 = 28
Alt. 2: Generell lösning
Summering i
varje kolumn ger svaret 10. Det innebär
minnes-
siffra i andra och tredje kolumnen från
vänster.
Därför är c + f = 10, b + e = 9 och a + d =
9
a + b +
c + d + e + f = 10 + 9 + 9 = 28
|
 |
|
|
Svar: 3
Lösning:
Antag att man startar med talet x.
Steg 1: 2x - 1
Steg 2: 2(2x - 1) -1 = 4x -3 =
22(x - 1) + 1
Steg 3: 2(4x - 3) - 1 = 8x - 7
= 23(x - 1) +
1
Steg n: 2n(x
- 1) + 1
Steg 99: 299(x
- 1) + 1
Ekv.: 299(x - 1) + 1 = 2100 + 1
299(x - 1) = 2100
Dividera med 299
x - 1 = 2
x = 3
|
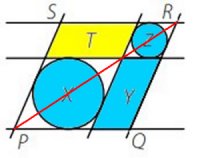
Svar: Det räcker att känna till arean
av området Y.
Lösning:
Alt. 1:
(Förslag av Staffan R.)
Om figuren speglas i linjen PR inser man
att arean T är lika stor som arean Y.
Alt. 2: (Förslag av Pelle P.)
Eftersom hela figuren PQRS blir en romb
i och med att
parallellogrammerna med cirkel X och Y blir romber,
så kommer T och Y båda ha samma längd på sina sidor
och samma innervinklar. Så T
är lika stor som Y.
|
 |
|
|
Svar:
Pyramidens
höjd är |
 |
Lösning:
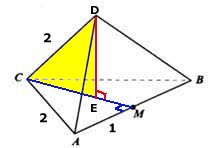
De fyra kulornas medelpunkter utgör hörnen i en
regelbunden tetraeder med kanten 2 cm. Tetraederns
botten ligger 1 cm ovanför marken och dess topp
1 cm under pyramidens högsta punkt.
Sträckan CM är
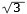 cm
(den längsta kateten i triangeln ACM. Höjden DE
delar medianen CM, så att cm
(den längsta kateten i triangeln ACM. Höjden DE
delar medianen CM, så att
CE:EM = 2:1. Därför är CD = 2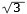 /3
cm /3
cm
Pythagoras sats på triangeln CDE ger
(DE)2 + (2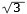 /3)2
= 22 /3)2
= 22
DE =
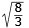
|
Pyramidens
höjd är |
 |
|
 |
|
|
Svar:
Det sista talet var 451
Lösning:
Summan av alla talen på tavlan var
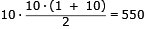
Varje gång två tal suddas ut, minskar
antalet tal på tavlan liksom talens summa med 1.
När bara ett tal återstår har antalet tal minskat
med 99. Då har också summan minskat med 99.
550 - 99 = 451.
|
|
|