Svar: 2 vägningar
Lösning:
Dela upp kulorna i tre högar och placera två av
högarna på var sin vågskål.
När man noterat resultatet, är det lätt att inse vad som
blir nästa vägning. |
|
Svar: 34 m stängsel
Lösning:
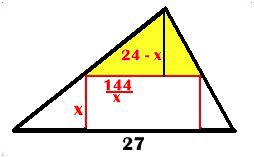
Den gula triangeln är likformig med hela
triangeln.
Med fig. beteckningar ger likformighet
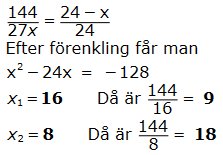
Stängsel till det rektangelformade området
behövs till tre sidor.
Alternativ 2 ger det kortaste stängslet:
8 m + 18 m + 8 m = 34 m |
 |
|
Bevis:
r .
(q!) = (q + 2)! - (q + 1)! |
Dividera i båda leden med
q! |
a) r = (q + 2)(q + 1)
- (q + 1)
|
|
Svar: |
Eftersom q
är ett positivt heltal och (q + 2)(q + 1)
> (q + 1) är
r också ett positivt heltal |
b) r = q2
+3q + 2 - q - 1
r = q2 +2q + 1
r = (q + 1)2 (q + 1)2
är ett perfekt kvadrattal!
| |
Svar: |
r är ett
perfekt kvadrattal |
|
|
Svar:
Efter fjärde omgången har
August vunnit 1 kr, Beda 13 kr och Christer 25 kr.
Lösning:
Antag att efter tredje omgången har August vunnit x
kr, Beda kx kr och Christer k2x kr.
Ekvationssystem: x + kx + k2x = 31
(1)
k2x - (kx + 8) = kx + 8 - x (2)
Aritmetisk serie
Förenkling av ekv. (2)
x(k2 -2kx +1) = 16
x = 16/(k2 -2kx +1)
x = 16/(k2 -2kx +1) insatt i ekv. (1) ger
efter förenkling
15 k2 - 78k +15 = 0
k1 = 5
(k2 = 1/5 duger inte eftersom den geometriska
serien är växande i
det här exemplet)
k = 5 insatt i ekv. (1) ger x + 5x + 25x = 31
x = 1
Efter fjärde omgången har
August vunnit 1 kr, Beda (5 + 8) kr = 13 kr och Christer
25 kr. |
|
|