|
Uppg.1: |
Svar: 25 cm och 7 cm
Lösning:
Vi börjar med att beräkna hypotenusan BC.
242 + 322 = (BC)2
576 + 1024 = (BC)2
(BC)2 = 1600
BC = ±
40
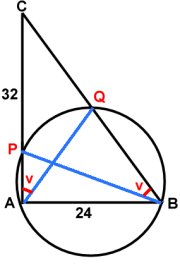
Då är CQ = QB = 20 cm
De vinklar som är betecknade med v i figuren är lika stora. (De
är bågvinklar (periferivinklar) på vinkel-bågen PQ. Enligt
bågvinkelsatsen är sådana vinklar lika stora.)
Vidare ingår vinkeln C i både triangeln ACQ och BCP.
Dessa trianglar är därför likformiga (likvinkliga trianglar).
Likformighet ger
PC/CQ = BC/AC
PC/20 = 40/32
PC = 25
Då är AP = 32 cm - 25 cm = 7 cm.
|
 |
|
Uppg.2: |
Bevis:
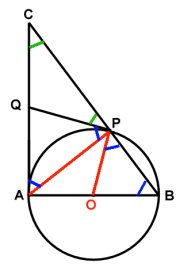
Låt O vara cirkelns medelpunkt och rita sedan in sträckorna
AP och OP i figuren.
Vinkeln OPQ är rät. (Tangenten är vinkelrät mot radien i
tangeringspunkten.)
Då är vinkeln APQ = 90o -
vinkeln APO.
Vinkeln APB är rät (bågvinkel på en halvcirkel)
Då är vinkeln OPB = 90o -
vinkeln APO.
Alltså är vinkeln APQ = vinkeln OPB (1)
Triangeln OBP är likbent.
Då kan vi utöka likheten (1)
Vinkeln APQ = vinkeln OPB = vinkeln PBO.
Trianglarna ABC och APC är likformiga.
Då är vinkeln PAC = vinkeln B.
Därav följer att triangeln APQ är likbent,
dvs. AQ = PQ (2)
Eftersom vinkeln APC är rät, och vi vet att vinkeln APQ =
vinkeln B, så är vinkeln CPQ = vinkeln C.
Då är triangeln CPQ likbent, dvs. PQ = CQ.
Då kan vi utöka likheten (2)
AQ = PQ = CQ Det innebär
att Q är mittpunkt på sträckan AC. |
 |
|