Ex. 2:
Svar:
Punkten ligger 1 dm från ena hörnet på sidan AB.
Lösning:
Givet:
x . y = 10
Längdenhet: dm
Sökt:
Sträckan AE.
Allmän lösning:
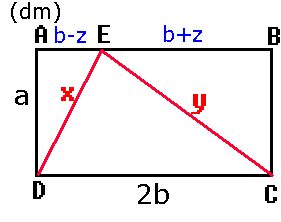
Sidan AD = a, sidan AB = 2b,
sträckan AE = b - z och
sträckan EB = b + z
Pytagoras sats ger:
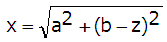
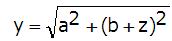
Efter förenkling får vi att
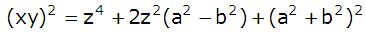
Dessutom vet vi att
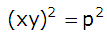 (I vårt exempel är p = 10)
(I vårt exempel är p = 10)
Ledvis subtraktion ger
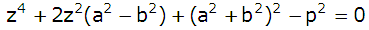
Lös ekv. med avseende på z2

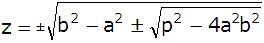
Specialfallet a = 2, b = 2,5 och p = 10 ger
z = ±
1,5
Fall 1: b - z = 2,5 - 1,5 = 1 och b + z = 2,5 + 1,5 =4
Fall 2: b - z = 2,5 - (-1,5) = 4 och b
+ z = 2,5 +(-1,5) = 1
Författaren till denna uppgift
har valt en rektangel där såväl sträckorna AE och EB som
produkten xy är rationella tal.
Ett annat exempel på en rektangel, där såväl sträckorna AE
och EB som produkten xy är rationella tal är en rektangel
med sidorna 24 och 50 l.e. och där produkten xy är 1200.
(AE = 18 l.e. och BE = 32 l.e. eller AE =
32 l.e. och BE = 18 l.e.)
OBS! Triangeln CDE är rätvinklig i detta exempel med sidorna
30, 40 och 50 l.e. |