|
Oxensvans |
|
Uppg. 1 |
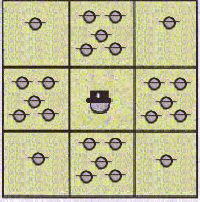Uppg. 2
 |
|
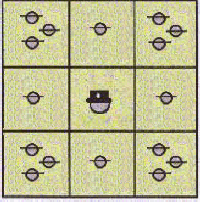Uppg. 3 |
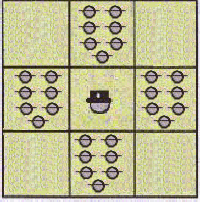Uppg. 4
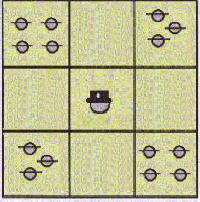
Svar: Man kan inkvartera
Svar: Man måste inkvartera
högst 28 soldater
minst 14 soldater (Soldater
endast i hörnrummen!)
Istället för kombinationen 4,3
går det naturligtvis också
med 7,0 6,1 eller 5,2. |
|
Uppg. 5 |
Ja!
Lösning |
|
Uppg. 6 |
Svar:
Gustaf Oxensvans föddes 1606.
Lösning: Det första villkoret är uppfyllt, om
åldern är 3, 12, 21, 30,
102, 111, 120, 201, 210 eller 300 år.
Åldrarna 12 och 201 uppfyller båda villkoren, men det är
ju inte rimligt att Oxensvans skulle vara över 200 år!
Trettioåriga kriget började 1618.
1618 - 12 = 1606. |
|
Uppg. 7 |
Svar:
En lösning är att
det från början fanns fyra soldater i varje hörnrum och en
soldat i vart och ett av de övriga rummen!
Lösning: Teoretiskt sett finns det oändligt många
lösningar till problemet, men naturligtvis utgör rummens storlek
en begränsning!
Antag, att det fanns x soldater i varje hörnrum och y soldater i
vart och ett av de övriga rummen.
Vid kontroll nr 1: Oxensvans räknar till (2x+y) soldater på
varje sida.
Vid kontroll nr 2: Oxensvans räknar till (x+2y) soldater på
varje sida.
Ekvation: 2*(2x+y)/3 = x+2y
Efter förenkling får man x = 4y, dvs. det var fyra
gånger så många soldater i ett hörnrum som i vart och ett av de
övriga rummen.
Det betyder att om y=1 är x= 4, om y=2 är x= 8...... |
|