Månadens problem
maj 2024 (lösning)
Uppgift 1:

 färjorna
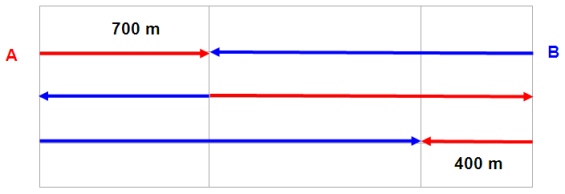
Svar: Avståndet mellan färjelägena är 1700 m.
 Lösning:
När färjorna möts första gången, 700 m från färjeläge A, har de tillsammans kört sträckan mellan färjelägena. När de möts nästa gång, 400 m från färjeläge B, är den sammanlagda sträckan tre gånger så lång som avståndet mellan färjelägena (se fig.). Den färja, som startade från A och är markerad med rött, måste då ha kört
3 . 700 m = 2100 m. Av figuren framgår att denna färja har kört sträckan mellan färjelägena och ytterligare 400 m.
 Avståndet mellan färjelägena är därför 2100 m - 400 m = 1700 m.
 
Uppgift 2:
parallelltrapetset
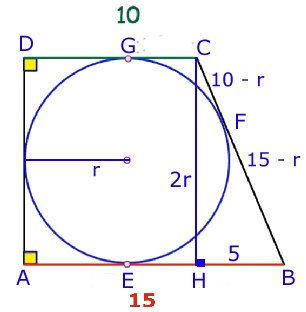
Svar: Cirkelns radie är 6 cm
Lösning:
Cirkelns radie är r cm.
Tangenterna
BE = BF = (15 - r) cm
CF = CG = (10 - r) cm

Hypotenusan BC i triangeln BCH är (25 - 2r) cm

Kateten CH = 2r i triangeln BCH

Kateten HB är (15 - 10) cm = 5 cm

Pythagoras sats på triangeln BCH ger
(2r)2 + 52 = (25 - 2r)2
4r2 + 25 = 625 - 100r + 4r2
100r = 600
    r = 6
 
Uppgift 3:

i potensform
Beräkna
Svara i potensform
(ej tiopotens).		 Svar: 16-2
Lösning:

Alternativt svar: 2-8
Förenkla 222 . 333
Skriv svaret som en potens.
Svar: 10811
Lösning:
 
Uppgift 4:

 lutande tornet i pisa
Svar:  Den sammanlagda sträckan är 218,777777... fot
Enligt Sam Loyd är detta exakt 218 fot 9 1/3 tum
 Lösning:
Första gången är fallhöjden 179 fot.
Andra gången studsar bollen 179 fot/10 och faller sedan samma sträcka, dvs.
Sammanlagt 35,8 fot
Fr.o.m. andra gången får vi en oändlig geometrisk serie med formeln
a/(1 - k)   a = 35,8   k = 10-1
Sammanlagd sträcka: 179 + 35,8/(1-0,1) = 218,777777... (fot)
 
Uppgift 5:

 STRÄCKAN EF

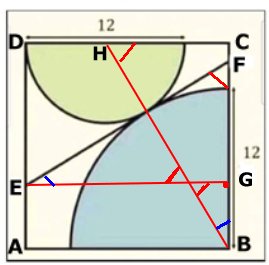
Svar: Sträckan EF är 18 cm.
Lösning:
 Av vinklarna framgår att trianglarna
 EFG och BCD är likformiga.
 Eftersom EG = BC (sidor i kvadraten) är trianglarna kongruenta.
 Därför är BH = EF.
 BH = 12 cm + 6 cm = 18 cm = EF

 

Tillbaka