Månadens problem
maj 2023
Uppgift 1:

PRICKARNA 
Svar:
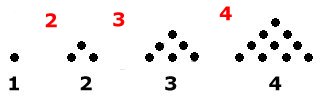
a) Fig. nr 5 har 15 prickar
b) Formeln är n(n + 1)/2
Lösning:
Formeln för aritmetsk summa:
 Sn = n . (a1 + an)/2
där a1 är första talet och an det n:te talet
(= det sista talet i summan)




Pricken i fig. 1 och de röda siffrorna bildar en aritmetisk serie. Antalet prickar i fig. nr n: n(1+n/2
 
Uppgift 2:
vinklarna
Svar:
Vinklarna v och u är lika stora, om summan av vinklarna a och c är lika med summan av vinklarna b och d.
 



Lösning:
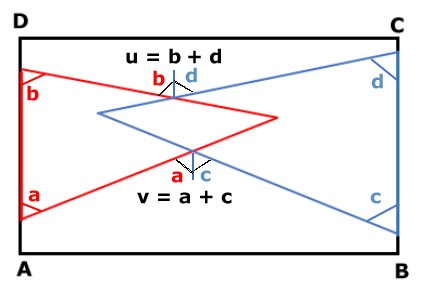Att v = a + c och u = b + d visar man med hjälp av satsen för alternatvinklar vid parallella linjer.
Detta gäller även om något av trianglarnas hörn sammanfaller med rektangelns hörn.
 
Uppgift 3:

Åkerfältet
Svar: a) b) c)
           
Skärningspunkten för de tre fälten delar höjden i förhållandet 2:1 i alla fallen.
Figur b
Här är varje röd linje parallell med en av sidorna.
Figur c
Förhållandet mellan areorna ska vara 7:6:5.
Pelle P. har föreslagit den här lösningen:
Den äldsta dottern får 3,5 små liksidiga trianglar (blått område)
Den mellersta dottern får 3 små liksidiga trianglar (rött område)
Den yngsta dottern får 2,5 små liksidiga trianglar (gult område)
Då är förhållandet 3,5:3:2,5 som kan skrivas 7:6:5.
 
Uppgift 4:

avståndet
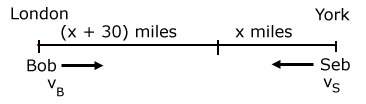
Svar: Avståndet mellan London och York är 150 miles.
Lösning:

 
Uppgift 5:

parallellogrammen
Bevisa att DA + AP = DC + CP

Bevis:
 Utnyttja att två tangenter från en punkt till en cirkel är lika långa samt att ABCD är en parallellogram.
AP = AE                   (1)
PC = CF                   (2)
BE = BF                   (3)
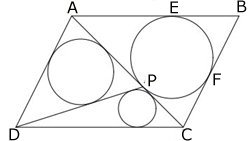DA + AB = DC + CB => DA + AE = DC + CF (eftersom BE = BF (3))
Men enligt (1) och (2) är AE = AP och CF = PC
Alltså är DA + AP = DC + PC
V.S.B
Extrauppgift:
Bevisa att / = AP/PC
Bevis:
1.  Areorna av trianglarna ADP och DCP förhåller sig som AP:PC.
(Lika stora höjder i trianglarna när AP resp. PC är bas).
2.  Areorna av trianglarna ADP och DCP är
(omkretsen av triangeln) . (den inskrivna cirkelns radie)/2
3.  För att bevisa att förhållandet mellan areorna av ADP och DCP = /, är det tillräckligt att visa att trianglarna APD och CPD har samma omkrets.
Vi bevisade  förra uppgiften att DA + AP = DC + PC.
Eftersom DP är gemensam för de båda trianglarna, har de samma omkrets!
Alltså är AP/PC = /
 

Tillbaka