Uppgift 1:
Svar: På Barrys åkermark är förhållandet mellan arean
för majs och arean för ärtor 11:9.
Lösning:
Antag att Angelas mark är 3x ha och Barrys mark är 2x
ha, dvs. sammanlagt 5x ha.
Sammanlagt gäller att M:Ä = 7:3 dvs.
majs odlas på 0,7 . 5x ha =
3,5x ha och ärter på (5x - 3,5x) = 1,5x
ha.
Angela har majs på 4/5 av sin jord, dvs. 4/5
. 3x = 2,4 x och ärter 1/5
. 3x = 0,6x
Barry har då majs på (3,5x - 2,4x) = 1,1x
och ärter på (1,5x - 0,6x) = 0,9x
Barry: Förhållandet mellan arean för majs och ärter =
1,1/0,9 = 11/9
|
|
Uppgift 2:
|
a)
Svar: 1898 var Sophie 22 år.
Lösning:
Antag att de två sista siffrorna i Sophies födelseår var
x(tiotal) och y(ental).
Då är Sophies ålder 1+ 8 + x + y = x + y + 9
Födelseår + Sophies ålder = 1898
Ekv.:
1800 + 10x + y + x + y + 9 = 1898
11x + 2y = 89
x = (89 - 2y)/11
Pröva genom att ersätta y med 0, 1, 2, ......, 9
Svar: y = 6 => x = 7 (Inga andra värden på y ger ett
heltalsvärde för x)
Sophie är född 1876 (siffersumma: 1 + 8 + 7 + 6 = 22)
Sophie är (1898 - 1876) år = 22 år
b)
Svar: 1889 var årtalets siffersumma dubbelt så stor som
Sophies ålder (13 är).
Lösning:
Från a-uppgiften vet vi att Sophie var född 1876.
Antag att siffersumman av årtalet 18ab är dubbelt så stor
som Sophies ålder det året.
Årtalet är 1800 + 10a + b med siffersumman
1 + 8 + a + b
Emmas ålder är då 1800 + 10a + b
-1876
Ekv.: 1 + 8 + a + b = 2(1800
+ 10a + b -1876)
9 + a + b = 20a + 2b - 152
19a = 161 - b
a = (161 - b)/19
0
≤
b
≤
9
Det heltaltal som närmast under 161 är delbart med 19 är
152.
162 - 9 = 152, så det betyder att b = 9
Svar: b = 9 => a = (161 - 9)/19 = 8
|
|
|
|
Uppgift 3:
|
Svar:
Avståndet mellan stationerna är 200
km
Lösning:
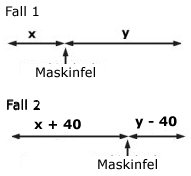
Fall 1
Maskinfelet inträffar efter x km.
Sträckan x km kör tåget normalt på 1 timme,
dvs. hastigheten är x km/h.
Efter maskinfelet är hastigheten 3x/4 km/h.
Tidsskillnaden mellan att köra med normal
och reducerad hastighet beror på sträckan
med maskinfel.
Uppgifterna i texten för fall 1 och fall 2
ger ekvationssystemet
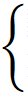 |
4y/3x = y/x
+1/2 (1)
4(y - 40)/3x = (y - 40)/x + 1/3
(2) |
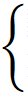 |
y =
1,5 x
y = 40 + x |
|
 |
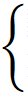 |
x =
80
y = 120
Avståndet mellan stationerna är (80
+ 120) km = 200 km
|
|
|
|
Uppgift 4: |
|
|
Svar: Summan av
vinklarna x och y
är 60o
Lösning:
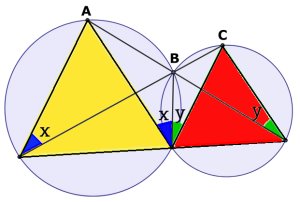
Skriv in de båda liksidiga trianglarna i var sin cirkel.
Vinklarna x är randvinkel på cirkelbågen
AB och därför lika stora.
Vinklarna y är randvinkel på cirkelbågen
BC och därför lika stora.
Vinkeln mellan de liksidiga trianglarna =
x + y = 180o - 60o - 60o
= 60o
(Uppg. konstruerad av Rony Sarker)
|
 |
|
|
|
Uppgift 5:
|
Svar:
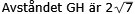
Lösning:
En liten finess gör lösningen enklare:
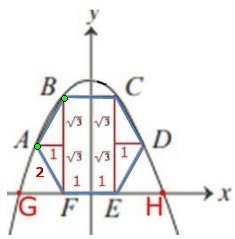
Figuren kan flyttas horisontellt så att y-axeln blir
symmetriaxel till figuren utan att avståndet GH påverkas.
Vinkelsumman i en månghörning med n hörn är
(n - 2) . 180o
Vinkelsumman i en hexagon (sexhörning) är
(6-2). 180o = 720o
Då är varje vinkel i en regelbunden hexagon
720o /6 = 120o
Dela upp hexagonen i halva liksidiga trianglar så som
figuren visar.
Kurvans ekvation är y = ax2 + bx + c
Vi behöver koordinaterna för tre punkter på kurvan för att
beräkna värdet av a, b och c.
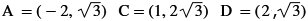
Ekvationssystem:

|
 |
|
|