Månadens problem
maj 2021
Uppgift 1:

En vinklad uppgift 
Svar: 180o.
Lösning:
Utnyttja yttervinkelsatsen!
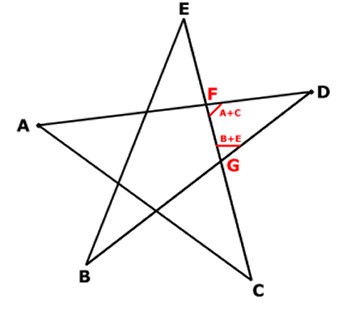
Vinkeln A + C (se figur) är yttervinkel till triangeln ACF.
Vinkeln B + E (se figur) är yttervinkel till triangeln BEG.

Vinkelsumman i en triangel är 180o.
I triangeln DFG är därför
A + C + D + B + E = 180o.
Uppgift 2:

 delbarhet
 Svar: 300 sexsiffriga tal.
 Lösning:
 Talen har formen abccba.
 Talen kan skrivas 100000a + 10000b + 1000c + 100c + 10b + a =
 100001a + 10010b + 1100c = 11(9091a + 910b + 100 c)
 Talet är alltså alltid delbart med 11.
 Vi söker alla sexsiffriga tal, som är delbara med 33. Det innebär att dessa tal 
 också ska vara delbara med 3.
 Om talet är delbart med 3, vet vi att talets siffersumma är delbar med 3, dvs. att 
 2a + 2b + 2c är delbart med 3, eller enklare a + b + c är delbart med 3.
 Det lägsta talet abc som är delbart med 3 är 102 och det högsta är 999.
 3 - 99: 99/3 = 33 naturliga tal delbara med 3.
 3 - 999: 999/3 = 333 naturliga tal delbara med 3.
 I Intervallet 102 - 999 finns det 333 - 33 = 300 tal delbara med 3
 
Uppgift 3:

stafetten
Svar:  
a) Varje löpare springer 900 m
b) Varje lag består av 9 löpare.
Lösning:
a)
Antag att hela loppet är x m.
Startmannen springer 100 m + (x - 100)/10 m
Löpare nummer 2 springer 200 m + (x - 100 - (x - 100)/10 - 200)/10 m
Ekv.:
100 + (x - 100)/10 = 200 + (x - 100 - (x - 100)/10 - 200)/10
Efter förenkling får man
10000 + 10x -1000 = 20000 + 10x - 3000 - x + 100
                        x = 8100
Startmannen springer 100 + (x - 100)/10 = 100 + 8000/10 = 900 (m)
b)
Antal löpare: 8100/900 = 9
Uppgift 4:

maximal area
Svar:
Maximal area för rektangeln är 96 cm2. 
Sidorna är då 10 cm och 9,6 cm.


Lösning:
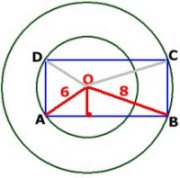
O är cirklarnas medelpunkt.
Arean av triangeln ABO = arean av triangeln CDO = 1/4 av rektangelns area, eftersom höjden i trianglarna är halva rektangelns höjd.
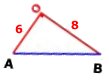
Triangeln ABO:s area är störst då vinkeln AOB = 90o (Se figur)
Arean av triangeln ABO är då 6.8/2 cm2 = 24 cm2  
och arean av rektangeln ABCD = 4 . 24 cm2 = 96 cm2

Sidan AB = 10 cm enligt Pythagoras sats på triangeln ABO.
Då är sidan AD = 96/10 cm = 9,6 cm.
Uppgift 5:

lamporna
Lösning:
 Slå på två strömbrytare och slå av den ena efter en stund.
Det ger följande alternativ beträffande hur lamporna är kopplade och vilken lampa som är trasig.
I. En lampa tänd och en annan varm. Då kan vi avgöra hur lamporna är kopplade samt att den kalla lampan är trasig.
II. En lampa tänd och de andra kalla. Skruva ur den tända lampan och en kall, och byt plats med dem. Vi kan då avgöra vilken av de släckta lamporna som fungerade, och som då aldrig varit påslagen, och vilken som var trasig, och som då varit kopplad till brytaren som slogs på och av.
III. Ingen lampa lyser, men en lampa är varm. Byt plats på de kalla lamporna för att avgöra hur lamporna är kopplade och vilken lampa som är trasig.

Tillbaka