Månadens problem
maj 2020 (lösning)
Uppgift 1:

prismat
Svar: x = 2
Lösning:
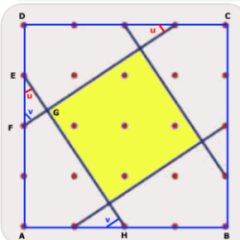
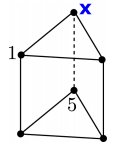
Summan av talen är 1 + 2 + 3 + 4 + 5 + 6 = 21. Summan utefter varje lodrät kant måste vara 21/3 = 7 för att villkoret om att summan av de fyra talen i varje kvadrat är lika ska vara uppfyllt. Alltså är x = 2
 
Uppgift 2:

järnvägsbron
Svar: 20  km/h
Lösning:
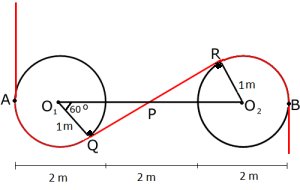
Antag att de springer med hastigheten x km/h samt att tåget befinner sig a km från bron,
som är 3b km lång.
 

Alt. 1: Att springa mot tåget (enligt formeln t = s/v)
          a/60 = b/x
Alt. 2: Att springa i samma riktning som tåget (enligt formeln t = s/v)
         (a + 3b)/60 = 2b/x
a/60 = b/x                     Multiplicera i båda leden med 2
(a + 3b)/60 = 2b/x
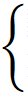2a/60 = 2b/x             
(a + 3b)/60 = 2b/x
  2a/60 = (a + 3b)/60     Efter förenkling får man a = 3b
Enligt alternativ 1 innebär det att tåget kör en sträcka som är tre gånger så lång som den som grabbarna springer. Deras hastighet är därför en tredjedel av tågets hastighet, dvs. 20 km/h.
 
Uppgift 3:

lägg på en rem 
Svar: ≈ 7,65 m
Lösning: Se figur till höger
Sträckan O1O2 är 4 m.
Då är sträckan O1P 2 m.
Triangeln O1PQ är en halv liksidig triangel.
Sträckan QP är då m
och QR 2 m
Cirkelbågarna AQ  och RB har medelpunktsvinkeln (180 - 60)o = 120o
Cirkelbågen AQ = RB är 2/3 m
Repet från A till B: m

 
Uppgift 4: 

ett högaktuellt problem
Svar: 2020
Lösning:
Vi börjar med att beräkna värdet av respektive term för x och y
x = 1 + 4 + 9 + 16 +  25 + 36 ...                              2020 termer
y =    3    + 8  + 15 + 24 + 35...  (2019 · 2021)    2019 termer

Jämför term 1 och term 2 i x med term 1 i y, därefter term 3 i x med term 2 i y osv.
I det första fallet är differensen 2. I alla övriga fall är differensen 1.
Därför är x - y = 2 + 2018 · 1 = 2020 
 
Uppgift 5:

fyrhörningen
 

a)
Bevis:
Triangeln EFG och triangeln AEH är likvinkliga och därmed likformiga.
Då är vinkeln EGF 90o. Vertikalvinkeln är också
90o. På motsvarande sätt kan vi visa att övriga vinklar i fyrhörningen är 90o.
Med hjälp av trianglar av typen AEH och EFG är det lätt att visa att fyrhörningen även är en kvadrat.
 
b)
Svar: ≈ 4,92 cm2
Lösning:
Arean är kvadraten ABCD - 4 . en triangel av typen AEH + 4 . en triangel av typen EFG
Kvadraten ABCD: 4 . 4 cm2 = 16 cm2
Triangeln AEH: 2 . 3/2 cm2 = 3 cm2
Antag att arean av triangeln EFG är A cm2
Areaskalan = (längdskalan)2
Jämför trianglarna EFG och AEH
Sidan EH är cm enligt Pythagoras sats
A/3 = ()2
A = 3/13
Den gula kvadratens area:
16 cm2 - 4 . 3 cm2 + 4 . 3/13 cm2 = ≈ 4,92 cm2
 
 

     Tillbaka