Månadens problem maj 2018

Månadens problem
maj 2018 (lösning)

Uppgift 1:
Svar: OTTO
Lösning: Namnet måste kunna spegelvändas.
Finns det något annat namn med fyra bokstäver, som har den egenskapen?
Ja, t.ex. namnet OMMO (variant av OMAR), som är ett pojknamn, men sannolikheten - åtminstone i Sverige - att någon heter OMMO är väl inte så stor.

Kommentar från Margit K.:
Bokstäver som kan förekomma är A, H, I, M, O, T, U, V, Å, Ä och Ö.
Första bokstaven måste vara en vokal och de två på mitten två lika konsonanter, annars låter namnet konstigt.
(X är också en symmetrisk bokstav min komm.)

Uppgift 2:
Svar: a + b = 50
Lösning: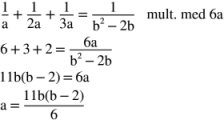

forts. från föregående spalt

a och b är positiva heltal.
Det minsta värdet på b, som ger ett positivt heltalsvärde på a, är b = 6
Då blir

a + b = 6 + 44 = 50

Uppgift 3:
Svar:
a) Vinkeln C är 45^o
b) Differensen mellan
vinklarna B och CAE är 45^o
Lösning:
Antag att höjden AD är h m.
Var och en av bröderna får en hektar = 10 000 m².
Ekv.: 100h/2 = 10000 h = 200
Det innebär att i triangeln ADC är
AD = DC = 200 m. Då är ACB 45^o

Triangeln ABE är likbent, dvs. vinkeln B = vinkeln AEB = v
Enligt yttervinkelsatsen för triangeln ACE är
v = u + 45
v - u = 45

Uppgift 4:
Bevis:
Bevisa att

Man kan få fram sambandet genom att utnyttja att trianglarna CDG och AFG är likformiga, men här ska vi titta på en annan metod:
Rita ut sträckan AC.
Arean av triangeln AFG = arean av triangeln ACG + arean av ACF.