Månadens problem april 2017

Månadens problem
maj 2017 (lösning)

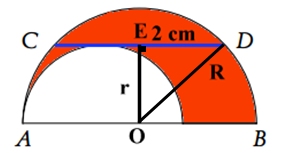
Uppgift 1:

Svar: Arean är 2cm²
Lösning:
R är radie i den större halvcirkeln och r i den mindre halvcirkeln.
O är medelpunkt i den större halvcirkeln.
Sträckan OE, som är vinkelrät mot CD, är lika lång som radien i den mindre halvcirkeln.

E är mittpunkt på kordan CD. Därför är sträckan ED 2 cm.
Pytagoras sats på triangeln DEO ger r² + 2² = R²R²-r² = 2²
Den röda arean : R²/2 - r²/2 = (R² - r²) ^. /2=
2² ^. /2 = 2
Anm.: Arean av det röda området (= 2) påverkas inte av radiernas längder.

Uppgift 2:
Svar:
a) När punkten P ligger i diagonalernas skärningspunkt är sammanlagda avståndet till rektangelns hörn så litet som möjligt, 20 cm. (se kalkyl nedan)
b) Största möjliga avstånd, 24 cm, får vi när punkten P ligger i ett av rektangelns hörn. (se kalkyl nedan)

Lösning:
Punkten P:s läge i förhållande till diagonalernas skärningspunkt framgår av figuren nedan.
Formeln för kalkylen i Excel ser ut så här:
= ROT((4-A2)^2+(3-B2)^2) + ROT((4+A2)^2 + (3-B2)^2) + ROT((4-A2)^2
+ (3+B2)^2) + ROT((4+A2)^2 + (3+B2)^2)

Hur genomför man ett bevis utan hjälp av kalkylprogram?

Sammanlagda avståndet:

Vi deriverar uttrycket ovan med avseende på x och y för att försöka hitta maximum och minimum.
Maximumvärdet är svårast att hitta, eftersom derivatan i hörnpunkten inte är noll.
Det finns dock en standardmetod för hur man ska hantera detta.