Näst högsta poängen?

Uppg. 1: Svar: 8 poäng Lösning: Segraren kan högst ha nio poäng. I så fall har han vunnit mot alla spelarna och tvåan kan då ha högst åtta poäng. Anm.: Tvåan kan inte ha 8½ poäng, för i så fall skulle ettan och tvåan båda ha 8½ poäng (efter remi i det inbördes partiet.)

Uppg. 2: Svar:  Alice hade 14 poäng. Lösning: Vi vet att ingen elev hade poängsummorna 0 eller 15. Då återstår sexton möjliga poängsummor (1 - 14 och 16 - 17). Men det var ju bara 15 elever. Finns det någon poängsumma som inte är tänkbar? Ja, poängsumman 16! Har en elev 16 tal på samma plats som läraren har, så måste ju också det sjuttonde talet finnas på samma plats. Den högsta poängsumman är därför 17 och den näst högsta 14. Anm.: Problemet är egentligen väldigt orealistiskt. På hur många olika sätt kan man ordna talen 1- 17? Svar: 17! 3,6 . 1014  (Ca 360 biljoner). Det är med andra ord mycket osannolikt att en elev skulle ha skrivit upp alla talen i samma ordning som läraren.
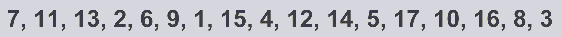