Lätt: Rum nr 1
Svar: 40 plattor eller 160 plattor av svart marmor
Lösning:
Alt.
1:
77
vita marmorplattor = 7 * 11 vita marmorplattor
Golvets mått är därför (7+2)(11+2)=9*13 plattor.
Antalet svarta plattor kan räknas ut på flera sätt:
2*9 + 2*13 -4 = 18 + 26 - 4 =40
2*8 + 2*12 = 16 + 24 = 40
9*13 - 77 = 117 - 77 = 40
Alt 2:
77
vita marmorplattor = 1 * 77 vita marmorplattor
(I praktiken kan väl ett rum knappast se ut på det
här sättet!)
Antalet svarta plattor:
3*79 - 77 = 160
|
 |
Medel: Rum nr 2
Svar: Golvet bestod av 1521 plattor
Lösning:
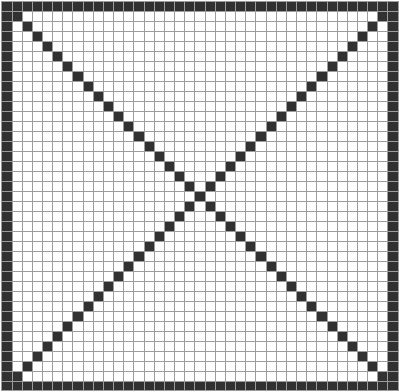
Om det ska ligga plattor som bildar en diagonal, måste
rummet vara kvadratformigt!
Före förändringen fanns det (4a - 4) svarta
marmorplattor.
a= antalet plattor längs en sida.
En diagonal innehåller (a-2) nya svarta plattor. Den andra
diagonalen bidrar med (a-3) plattor, eftersom plattan
i mitten redan är medräknad i den första diagonalen.
Ekv.: (4a - 4) +(a - 2) + (a - 3) =225
6a - 9 = 225
a = 39
Antal plattor: 39 * 39 = 1521
|
Svår: Rum nr 3 |
Svar: Golvet bestod av 8648 vita plattor.
|
|
Lösning: |
|
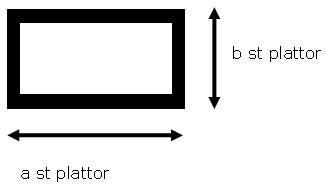
Antal svarta plattor:
2a +2b -4
Antalet vita plattor: (a-2)(b-2) |
 |
Ekv.:
(a-2)(b-2) = 23 (2a + 2b -4)
ab - 2a - 2b + 4 = 46 a + 46 b - 92
ab - 48a - 48b = - 96
a(b - 48) = 48(b - 2)
a = 48(b - 2)/(b - 48)
Vi vet att a <100, dvs. 48(b - 2)/(b - 48)<100
Efter förenkling får man 13 b>1176
b> 90,...
Det innebär att b ligger i intervallet 90<b<100
Eftersom a och b är naturliga tal är lösningen enkel att
hitta.
b = 94 ger a = 48(b - 2)/(b - 48) =
48*92/46 = 96
b = 96 ger a = 48(b - 2)/(b - 48) =
48*94/48 = 94
OBS! Samma värden i båda lösningarna men med ombytta
värden för a och b.
Anm.: Eftersom det fanns 23 gånger så många vita
plattor som svarta, måste antalet plattor vara
delbart med 24. Därför måste ett av värdena för a
resp. b vara delbart med 24.
Antal vita plattor: 94*92 = 8648 |
|