Lika stora men ändå så olika! (Lösning)

Uppgift 1

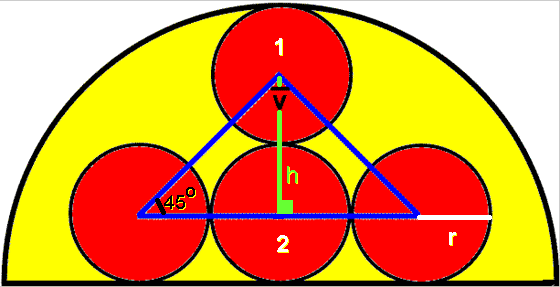
a) Radien i de röda cirklarna är r l.e. Då är radien i den gula halvcirkeln 4 * r l.e. = 4r l.e. (Det framgår av cirklarna 1 och 2) Den gula halvcirkelns area är då = 4r * 4r *p/2 a.e. = 8r2p De röda cirklarnas area: 4*r * r *p = 4r2p a.e. De gula områdena area: 8r2p a.e. - 4r2p a.e. = 4r2p a.e.  V.S.B. b) Höjden  (h) i den blå triangeln delar denna i två likbenta, rätvinkliga trianglar med katetrarna 2r l.e. Vinkeln v är därför 45o + 45o = 90o   V.S.B.

Uppgift 2

Lösningen bygger på att man inser, att vinkeln v är 90o eftersom den är periferivinkel (randvinkel) på halvcirkelbågen med c som diameter. Pytagoras sats ger därför a2 + b2 = c2 som kan skrivas a2 + b2 - c2 = 0 (1) Arean av halvcirkeln med a som diameter: a2 *p/8 a.e  Arean av halvcirkeln med b som diameter: b2 *p/8 a.e  Arean av halvcirkeln med c som diameter: c2 *p/8 a.e  Vi antar att triangelns area är T a.e. De röda månskärornas area blir då a2 *p/8 a.e + b2*p/8 a.e  - c2*p/8 a.e + T a.e. = p/8(a2 + b2 - c2) a.e + T a.e. = T a.e. (eftersom a2 + b2 = 0 enl. ekv. (1)) V.S.B.

Uppgift 3   I fig. finns det en kvartscirkel med radien 2r l.e. och två halvcirklar med radien r l.e. Arean av området H får man genom att ta arean av kvartscirkeln - arean av de båda halvcirklarna + arean av området G (eftersom området G ingår i båda halvcirklarna). Arean av området H: (4r2p/4 - 2*r2p/2 + G) a.e. = (r2p - r2p + G) a.e. = G a.e. V.S.B.

Tillbaka