|
DUELLEN |
a)
Svar:
Rasmus
vinner.
Lösning:
När Lukas har sprungit 95 m, har Rasmus sprungit 100 m, dvs.
de är jämsides, eftersom Rasmus startade 5 m bakom
Lukas.
De sista fem meterna springer Rasmus snabbare, eftersom
han har högre hastighet.
b)
Svar: Rasmus ska starta (avrundat) 5,263 m bakom
startlinjen.
Lösning:
Antag att Rasmus har hastigheten v m/s och att han
startar x m bakom startlinjen.
Lukas springer 95 m, när Rasmus springer 100 m. Hans
hastighet är då 0,95v m/s.
Tiden för Rasmus blir (100 + x)/v sekunder. Tiden för
Lukas blir 100/0,95v sekunder
De kommer samtidigt i mål.
Det ger ekvationen (100 + x)/v = 100/0,95v
Multiplicera med 0,95v i båda leden
Efter förenkling får man
95 +0,95x = 100
0,95x = 5
x = 5,263...
|
|
|
|
|
multiplikationen |
Svar:
| |
1 |
0 |
2 |
5 |
6 |
4 |
|
* |
|
|
|
|
|
4 |
| |
4 |
1 |
0 |
2 |
5 |
6 |
Lösning:
Sätt talet PQRST = x
Talet PQRST4 har då värdet 10x + 4
Multiplikationen kan då skrivas 4(10x +4) = 400000 + x
40x + 16 = 400000 + x
39x = 399984
x = 10256
|
|
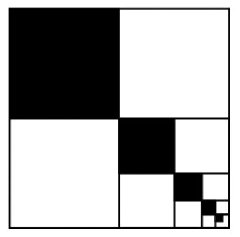
KVADRATERNA
|
Svar: Den
sammanlagda arean är 28 cm2
Lösning:
Metod 1:
Oändligt många svarta kvadrater.
För varje svart kvadrat, finns det två vita kvadrater av
samma storlek, en till höger om den och en rakt under
den.
Alltså utgör de svarta kvadraterna en tredjedel av hela
figurens area.
84 cm2/3 = 28 cm2
Metod 2: En oändlig geometrisk serie.
Formel: s = a1 /(1 - k) -1
< k < 1
I det här fallet är a1
= den största svarta kvadraten =84 /4 =
21
k = kvoten mellan en term och närmast föregående
term.
k =
1/4 (Arean av den andra svarta kvadraten är
1/4 av arean av den första svarta kvadraten)
|
s =
a1 /(1 - k) = 21/(1 - 1/4) = 28 |
|
|
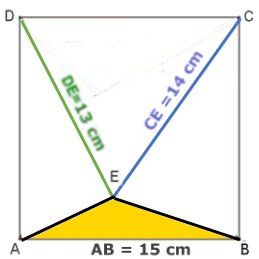
AREAN AV TRIANGELN ABE |
Svar: Arean
av triangeln ABE är
28,5 cm2
Lösning:

Triangeln CDE:s
area
p = 21 cm

Man kan lätt bevisa att arean av
triangeln CDE och arean av triangeln
ABE är hälften av kvadratens area.
Då är arean av triangeln ABE =
15 . 15/2 - 84 = 28,5 (cm2)
|
 |
|
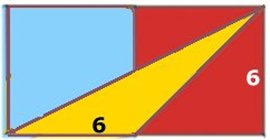
DEN GULA TRIANGELNS AREA |
Svar: Den
gula triangelns area är
18 cm2
|
 |
Lösning:
Den blå kvadraten är större än den röda kvadraten.
Om vi tittar på gränsvärdet när kvadraterna är lika stora ser
det ut så här (se fig. ovan):
Arean är då 18 cm2
|
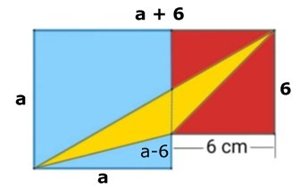
Det gäller nu att undersöka om den gula arean
alltid är 18 cm2, när den blå kvadraten är större än
den röda.
Den blå + den röda kvadraten: a2 + 36 (cm2)
Den del av kvadraterna som inte täcks av den gula triangeln:
a(a + 6)/2 + 6 . 6/2 + a(a - 6)/2 = (a2
+ 6a)/2 + 18 + (a2 - 6a)/2 (cm2)
Då är den gula triangelns area:
a2 + 36 - (a2/2
+ 3a + 18 + a2/2 - 3a) = 18 (cm2) |
 |