Månadens problem juni 2022

det tresiffriga talet

Svar: Talet x kan se ut på 40 olika sätt.
Lösning:
Talet x har värdet 100a + 10 b + c och talet y har värdet 100c + 10 b + a
x - y = 100a + 10 b + c -(100c + 10 b + a) = 99a - 99c =
99(a - c)
Vi vet också att x - y = 495, dvs.
99(a - c) = 495 Dividera i båda leden med 99
a - c = 5 a≠ 0 c≠ 0 eftersom talen är tresiffriga.
a kan anta 4 värden: 6, 7, 8 och 9
(för att uppfylla villkoret a - c = 5) och
b kan anta 10 värden: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Det ger sammanlagt 4 ^. 10 möjligheter = 40 möjligheter

GODSTÅGET

Svar: Godståget är 240 m
Lösningsförslag 1:
När godståget har passerat Brita, har Adam (precis som Brita) gått 30 m.
När godståget passerar Adam har han gått ytterligare 10 m.
Under samma tid har godståget kört 30 m + 30 m + 10 m = 70 m (se figur).

Tågets hastighet är alltså 7 gånger så stor som Adams och Britas hastighet.
Under tiden som Adam gått 40 m, har tåget kört 7 ^. 40 m = 280 m.
Godstågets längd är därför 280 m - 40 m = 240 m

Lösningsförslag 2:
   Antag att tågets längd är x m. Hastigheten är v_T Adams och Britas hastighet är v_AB Ekvationssystem: Sträckorna är proportionella mot hastigheterna
(x - 30)/30 = v_T/v_AB
(x + 40)/40 = v_T/v_AB

Då får vi ekvationen
(x - 30)/30 = (x + 40)/40
   x = 240

primtalen

a)
Svar: (Ett primtal > 3)²- 1är alltid jämnt delbart med 24
Lösning:
Antag att primtalet är x (x> 3)
● Kvadraten på primtalet minskat med 1 är då x² - 1 = (x + 1)(x - 1)
● Ett primtal är alltid ett udda tal (med undantag för talet 2, som är ett primtal).
    Då är (x + 1) och (x - 1) jämna tal.
● Ett av dem är delbart med 2 och det andra är delbart med 4.
● Av tre på varandra följande positiva heltal är ett av talen delbart med 3.
   Men primtal större än 3 är inte delbart med 3. Då är antingen (x + 1) eller (x - 1)
   delbart med 3.
Slutsats: x² - 1 är delbart med 2^.3 ^. 4 = 24

b)
Svar: Summan av två primtalstvillingarär alltid jämnt delbar med 12
Lösning:
Antag att primtalstvillingarna är x - 1 och x + 1 (och heltalet mellan dem är x)
● Då är summan av dem 2x.
● Av tre på varandra följande positiva heltal är ett av talen delbart med 3.
   Inget av primtalen (>3) är delbart med 3. Alltså är x jämnt delbart med 3.
● x ligger mellan två udda tal och är ett jämnt tal och därför jämnt delbart med 2.
● x är alltså jämnt delbart med 2^.3
● Slutsats: 2x är jämnt delbart med 2^.2^.3 = 12

logaritmer

Svar: 3log6 - 2log2
Lösning:

kuben

Svar:
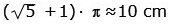
Lösning:
När kuben roterar 90 grader, rör sig punkten
längs bågen av en cirkelsektor med
medelpunktsvinkeln 90 grader.
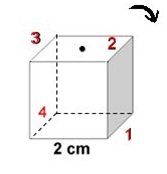
Kuben vrids i tur och ordning längs kanterna
1, 2, 3 och 4 ( figur till höger).
När kuben vrids längs kanterna 1 och 4,
beräknas cirkelsektorns radie med Pytagoras
sats enligt fig. 1
När kuben vrids längs kanterna 2 och 3, blir
cirkelsektorns radie 1 cm enligt fig. 2

Punkten rör sig