|
papperslappen |
|
a)
Svar: På papperslappen stod det (3 . 234)2
= 492804
Lösning:
Antag
att den oläsliga siffran i vänstra ledet är x
(3(230 + x))2 i vänstra ledet kan skrivas
32
. (230 + x)2 . Därför är vänstra
ledet delbart med 9. Då är också högra ledet delbart med 9.
Det finns en regel som anger att även siffersumman då är delbar med 9.
Siffersumman i högra ledet är 4 + 9 + 2 + x + 0 + 4 = 19 + x.
Det närmast högre talet som är delbart med 9 är 27. Då är x = 27
- 19 =
8
Den saknade siffran i vänstra ledet kan beräknas så här:
Eftersom kvadraten 492804 slutat med siffran 4, måste talvärdet
i parentesen i vänstra ledet sluta på 2 eller 8.
3 . 234 = 702 och 3 .
236 = 708.
De två sista siffrorna i 492804 är 04. Det får man om man tar
7022.
Den oläsliga siffran i parentesen är 4.
b)
Svar: Det finns två lösningar:
1) x = 4 och y = 8
2) x = -464 och y = 8
Lösning:
y = 8 enl. samma resonemang som i uppg. a.
Beräkning av x
492804/9 = 54756
(230 + x)2 = 54756
230 + x = ± 234
x1 = 4 x2 = - 464
|
|
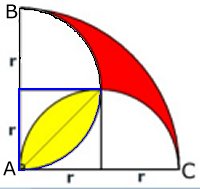
areorna
|
Bevis:
Sidan AB = sidan BC = 2r
Den gula arean |
 |
●
●
|
Börja med att beräkna halva den
gula arean = kvartscirkeln (markerad med blått) - halva
kvadraten = r2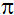 /4
- r2/2 /4
- r2/2
Hela den gula arean:
2(r2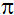 /4
- r2/2)
= r2( /4
- r2/2)
= r2(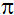 /2
- 1) /2
- 1) |
Den röda arean |
|
● |
Den röda arean = Den stora
kvartscirkeln - de vita kvartscirklarna - kvadraten =
(2r)2 . 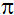 /4
- r2 . /4
- r2 . 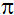 /2
- r2
= r2 . /2
- r2
= r2 . 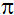 /2
- r2
= /2
- r2
=
=
r2(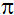 /2 -
1) V.S.B /2 -
1) V.S.B |
|
talserien |
Svar: Talen är 24, 32,
24, 24, 20 och 18 eller 56, 16, 32, 20, 22 och 17.
Lösning:
Antag att det tredje talet är x.
Villkoret tn
+ 2 .
tn+1 = 96 - 8n ger då följande beteckning för de
sex talen:
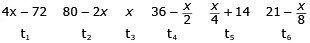
Av t1 och t2 framgår att 18 < x <
40
Enligt t6 ska x också vara jämnt delbart med 8.
Det finns två tal mellan 18 och 40, som uppfyller det
villkoret, nämligen 24 och 32.
Alternativ 1:
x = 24 => 24 32 24 24
20 18
Alternativ 2:
x = 32 => 56 16 32 20 22
17
|
|
fåren |
a)
Svar: Det minsta antalet är 301 får.
Lösning:
Det minsta positiva tal som ger ett heltalssvar vid
division med 2, 3, 4, 5 och 6 är 60.
Då undersöker vi för vilket värde på n som 60
. n + 1 är delbart med 7
60 . 1 + 1 = 61
61/7
Ï
N
60 . 2 + 1 = 121
121/7
Ï
N
60 . 3 + 1 = 181
181/7
Ï
N
60 . 4 + 1 = 241
241/7
Ï
N
60 . 5 + 1 = 301
301/7 =
43
b)
Svar: Antalet får är 60n + 1 n = 5,
12, 19 ...
Lösning:
Från uppgift a) vet vi att 60n + 1 är en lösning,
då n = 5
Om 60n + 1 är en
lösning, måste 60(n + 7) + 1 = 60n
+ 1 + 7 . 60 vara en lösning.
Allmänt gäller då att antalet får är 60n + 1 n =
5, 12, 19 ...
|
|
Sockerblandningen |
Svar: x + v + b = 48
Lösning:
Vi startar med 320 g vitt socker och 0 g brunt socker i
skålen.
Blandning A:
(320 - x) g vitt socker och x g brunt socker
Förhållande: (320 - x)/x = v/b
Blandning B: Förhållande: vitt socker/brunt socker =
49/15
I blandning B finns det då 320 .
49/(49 + 15) g vitt socker = 245 g
vitt socker och (320 -
245 ) g brunt socker = 75 g brunt socker (1)
För att få en ekvation måste vi kunna ange mängde
brunt socker i
blandning B med hjälp av x.
I blandning A finns x g brunt socker av sammanlagt 320
g socker.
Blandning B: x gram tas bort från blandning A. Då
tar man bort x/320 av x
g brunt socker och lägger sedan till
x
gram brunt socker.
Totalt: x -
x . x/320 +
x
= 2x - x2/320
(2)
(1) och (2) ger ekvationen
2x - x2/320 = 75
x2 - 640x + 24000 = 0
x1 = 600 Duger ej eftersom x < 320
x2 = 40
I blandning A fanns det därför 40 g brunt socker och (320 -
40) g = 280 g vitt socker. Då är v/b = 280/40 = 7/1 (7 : 1),
dvs. v = 7 och b = 1
x + v + b = 40 + 7 + 1 = 48
|
|